��Ŀ����
4�������˶�������һ������Ŀ��ͼ��ʾ���˶�Ա���ڱ��ܵ����ϣ��乭�ż��������Ĺ̶�Ŀ�꣮�����˶�Ա�������۵��ٶ�Ϊv1���˶�Ա��ֹʱ����Ĺ����ٶ�Ϊv2���ܵ���̶�Ŀ����������Ϊd��Ҫ������Ŀ��������ļ��ڿ��з���ʱ����̣�������| A�� | �˶�Ա�ż�����Ŀ��ľ���Ϊ$\frac{d{v}_{2}}{{v}_{1}}$ | |
| B�� | �˶�Ա�ż�����Ŀ��ľ���Ϊ$\frac{d\sqrt{{{v}_{1}}^{2}+{{v}_{2}}^{2}}}{{v}_{2}}$ | |
| C�� | ���䵽�̶�Ŀ������ʱ��Ϊ$\frac{d}{v_1}$ | |
| D�� | ���䵽�̶�Ŀ������ʱ��Ϊ$\frac{d}{\sqrt{{{v}_{2}}^{2}-{{v}_{1}}^{2}}}$ |
���� �˶�Ա�ų��ļ��Ȳ������������з����ϵ�����ֱ���˶����ֲ����˴�ֱ�������з����ϵ�����ֱ���˶������ų��ļ���ֱ�������з����䣬��ʱ����ʱ����̣�����t=$\frac{d}{{v}_{2}}$ ������ʱ�䣬���ݷ��˶��ͺ��˶����е�ʱ�ԣ�������������з����ϵľ��룬�����˶��ĺϳɣ�����˶�Ա�ż�����Ŀ��ľ��룮
��� �⣺AB�����ʱ��Ϊt=$\frac{d}{{v}_{2}}$��������������з����ϵ�λ��Ϊx=v1t=$\frac{{v}_{1}d}{{v}_{2}}$�����Էż�������Ŀ��ľ���Ϊs=$\sqrt{{d}^{2}+��\frac{{v}_{1}d}{{v}_{2}}��^{2}}$=$\frac{d\sqrt{{{v}_{1}}^{2}+{{v}_{2}}^{2}}}{{v}_{2}}$����A����B��ȷ��
CD�����ų��ļ���ֱ�������з����䣬��ʱ����ʱ����̣��������ʱ��t=$\frac{d}{{v}_{2}}$����CD����
��ѡ��B��
���� �������Ĺؼ�֪�����������������з����ϵ�����ֱ���˶��ʹ�ֱ�������з����ϵ�����ֱ���˶���֪�����˶�����˶����е�ʱ�ԣ�

��ϰ��ϵ�д�
 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
�����Ŀ
14�� ��ͼ��R��Ϊ�������裬���������������ֵ�㶨��CΪ���������պϿ���Sһ��ʱ����ù������������ʱ��������
��ͼ��R��Ϊ�������裬���������������ֵ�㶨��CΪ���������պϿ���Sһ��ʱ����ù������������ʱ��������
 ��ͼ��R��Ϊ�������裬���������������ֵ�㶨��CΪ���������պϿ���Sһ��ʱ����ù������������ʱ��������
��ͼ��R��Ϊ�������裬���������������ֵ�㶨��CΪ���������պϿ���Sһ��ʱ����ù������������ʱ��������| A�� | ��������ʾ������ | B�� | ��������ʾ����С | ||
| C�� | �������Ĵ�������С | D�� | �������Ĵ��������� |
15���ÿ������ż������۲�����������ʱ������˵��������ǣ�������
| A�� | �������ƿ���������������խ���� | |
| B�� | ���Ϲ�����Դʱ�۲쵽�����Ʊ��ú������Դʱ�۲쵽�����ƿ� | |
| C�� | �ð�����Դʱ��������ְ�ɫ���ƣ�����Ϊ��ɫ���� | |
| D�� | �������������0.5mm��С��0.2mm�����Ƽ���������ȱ䰵 |
12��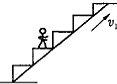 ��ͼ��ʾ���Զ������Ժ㶨���ٶ�v1��ת��������Ա��¥��ij�˵�һ��վ�������Ϻ���Է��ݾ�ֹ����������������¥����������ΪW1����������ΪP1���ڶ����������˶��ķ�����������Է��ݵ��ٶ�v2ͬʱ���������ߣ���η�������W2����������P2��������˵������ȷ���� ��������
��ͼ��ʾ���Զ������Ժ㶨���ٶ�v1��ת��������Ա��¥��ij�˵�һ��վ�������Ϻ���Է��ݾ�ֹ����������������¥����������ΪW1����������ΪP1���ڶ����������˶��ķ�����������Է��ݵ��ٶ�v2ͬʱ���������ߣ���η�������W2����������P2��������˵������ȷ���� ��������
 ��ͼ��ʾ���Զ������Ժ㶨���ٶ�v1��ת��������Ա��¥��ij�˵�һ��վ�������Ϻ���Է��ݾ�ֹ����������������¥����������ΪW1����������ΪP1���ڶ����������˶��ķ�����������Է��ݵ��ٶ�v2ͬʱ���������ߣ���η�������W2����������P2��������˵������ȷ���� ��������
��ͼ��ʾ���Զ������Ժ㶨���ٶ�v1��ת��������Ա��¥��ij�˵�һ��վ�������Ϻ���Է��ݾ�ֹ����������������¥����������ΪW1����������ΪP1���ڶ����������˶��ķ�����������Է��ݵ��ٶ�v2ͬʱ���������ߣ���η�������W2����������P2��������˵������ȷ���� ��������| A�� | W1��W2 P1��P2 | B�� | W1��W2 P1=P2 | C�� | W1=W2 P1��P2 | D�� | W1=W2 P1=P2 |
9�����ڵ��ɣ�����˵����ȷ���ǣ�������
| A�� | ��������Ĵ�С�Ծ�����������Ӱ���ܹ����Բ���ʱ����Ϊ���� | |
| B�� | ��Ϊ���Ӻ�С�����Ե������κ�ʱ���Կ������� | |
| C�� | ������������ϴ��κ�ʱ���ܿ������� | |
| D�� | ���ɾ���ֻ��������û�д�С�ĵ� |
16�� һ��С����б�������˶�����ÿ��$\frac{1}{10}$s�ع�һ�ε�Ƶ��������㲻ͬʱ��С��λ�õ���Ƭ����ͼ��ʾ������Ƭ�ϳ��ֵ���������С�����֮���ʱ����Ϊ$\frac{1}{10}$s�����С�����ĸ��������ʱ����λ�����ݼ�����
һ��С����б�������˶�����ÿ��$\frac{1}{10}$s�ع�һ�ε�Ƶ��������㲻ͬʱ��С��λ�õ���Ƭ����ͼ��ʾ������Ƭ�ϳ��ֵ���������С�����֮���ʱ����Ϊ$\frac{1}{10}$s�����С�����ĸ��������ʱ����λ�����ݼ�����
��1��С��ļ��ٶ�Ϊ1.10m/s2��
��2��ͼ��С����λ����͵����ٶ�Ϊ1.32m/s�������������������Ч���֣���
 һ��С����б�������˶�����ÿ��$\frac{1}{10}$s�ع�һ�ε�Ƶ��������㲻ͬʱ��С��λ�õ���Ƭ����ͼ��ʾ������Ƭ�ϳ��ֵ���������С�����֮���ʱ����Ϊ$\frac{1}{10}$s�����С�����ĸ��������ʱ����λ�����ݼ�����
һ��С����б�������˶�����ÿ��$\frac{1}{10}$s�ع�һ�ε�Ƶ��������㲻ͬʱ��С��λ�õ���Ƭ����ͼ��ʾ������Ƭ�ϳ��ֵ���������С�����֮���ʱ����Ϊ$\frac{1}{10}$s�����С�����ĸ��������ʱ����λ�����ݼ�����| x1/cm | x2/cm | x3/cm | x4/cm |
| 8.20 | 9.30 | 10.40 | 11.50 |
��2��ͼ��С����λ����͵����ٶ�Ϊ1.32m/s�������������������Ч���֣���
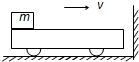 ����M��С����˷�������m�����飬�Թ�ͬ�ٶ�v�ع⻬ˮƽ������ֱǽ�˶�������ǽ��ײ��ʱ�伫�̣����ƶ�����ʧ����ͼ��ʾ��С��������Ķ�Ħ������Ϊ�̣�С���㹻�������鲻�ᵽ�ﳵ���Ҷˣ�����С����������Ծ�ֹ���������������������Ħ�������������Ƕ��٣�
����M��С����˷�������m�����飬�Թ�ͬ�ٶ�v�ع⻬ˮƽ������ֱǽ�˶�������ǽ��ײ��ʱ�伫�̣����ƶ�����ʧ����ͼ��ʾ��С��������Ķ�Ħ������Ϊ�̣�С���㹻�������鲻�ᵽ�ﳵ���Ҷˣ�����С����������Ծ�ֹ���������������������Ħ�������������Ƕ��٣�