题目内容
13.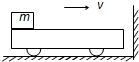 质量M的小车左端放有质量m的铁块,以共同速度v沿光滑水平面向竖直墙运动,车与墙碰撞的时间极短,不计动能损失,如图所示.小车与铁块的动摩擦因数为μ,小车足够长,铁块不会到达车的右端,最终小车与铁块相对静止.求以下三种情况下由于摩擦产生的热量是多少?
质量M的小车左端放有质量m的铁块,以共同速度v沿光滑水平面向竖直墙运动,车与墙碰撞的时间极短,不计动能损失,如图所示.小车与铁块的动摩擦因数为μ,小车足够长,铁块不会到达车的右端,最终小车与铁块相对静止.求以下三种情况下由于摩擦产生的热量是多少?(1)M>m
(2)M=m
(3)M<m.
分析 车与墙碰后瞬间,小车的速度向左,大小是v,而铁块的速度未变,仍是v,方向向右.根据动量守恒定律,车与铁块相对静止时的速度方向决定于M与m的大小关系,分三种情况,根据动量守恒定律以及能量守恒定律列式求解即可.
解答 解:(1)当M>m时,相对静止的共同速度必向左,不会再次与墙相碰,以初速度方向为正,
根据动量守恒定律:Mv-mv=(M+m)v′
摩擦产生的热量是:$Q=\frac{1}{2}(M+m){v^2}-\frac{1}{2}(M+m){v^{/2}}$
解得:$Q=\frac{2Mm{v}^{2}}{M+m}$
(2)当M=m时,显然碰后达到的最终共同速度为零,同时停止运动.摩擦产生的热量等于系统的初动能:为$Q=\frac{1}{2}(M+m){v}^{2}$
(3)当M<m时,相对静止时的共同速度必向右,多次与墙相碰,直到小车停在墙边,摩擦产生的热量等于系统的初动能:$Q=\frac{1}{2}(M+m){v}^{2}$
答:(1)M>m时由于摩擦产生的热量是$\frac{2Mm{v}^{2}}{M+m}$;
(2)M=m 时由于摩擦产生的热量是$\frac{1}{2}(M+m){v}^{2}$;
(3)M<m时由于摩擦产生的热量是$\frac{1}{2}(M+m){v}^{2}$.
点评 本题涉及到两个物体的相互作用,应优先考虑动量守恒定律.运用动量守恒定律研究物体的速度,比牛顿第二定律和运动学公式结合简单,因为动量守恒定律不涉及运动的细节和过程.涉及时间问题,可优先考虑动量定理.

练习册系列答案
相关题目
3.关于点电荷和元电荷,下列说法正确的是( )
| A. | 自然界把电荷按不同属性分成两类:正电荷、负电荷或点电荷、元电荷 | |
| B. | 因为电子很小,所以电子在任何时候都可以看作点电荷 | |
| C. | 当带电体的大小对静电作用力的影响能够忽略不计时可视为点电荷 | |
| D. | 元电荷就是电子和质子 |
4.民族运动会上有一骑射项目如图所示,运动员骑在奔跑的马上,弯弓放箭射击侧向的固定目标.假设运动员骑马奔驰的速度为v1,运动员静止时射出的弓箭速度为v2,跑道离固定目标的最近距离为d.要想命中目标且射出的箭在空中飞行时间最短,则( )
| A. | 运动员放箭处离目标的距离为$\frac{d{v}_{2}}{{v}_{1}}$ | |
| B. | 运动员放箭处离目标的距离为$\frac{d\sqrt{{{v}_{1}}^{2}+{{v}_{2}}^{2}}}{{v}_{2}}$ | |
| C. | 箭射到固定目标的最短时间为$\frac{d}{v_1}$ | |
| D. | 箭射到固定目标的最短时间为$\frac{d}{\sqrt{{{v}_{2}}^{2}-{{v}_{1}}^{2}}}$ |
8.船在静水中的速度是1m/s,河岸笔直,河宽恒定,靠近岸边河水的流速为2m/s,河中间河水的流速为3m/s,以下说法正确的是( )
| A. | 因船速小于水流速,船不能到达对岸 | |
| B. | 船不可能沿一直线过河 | |
| C. | 船可能到达正对岸 | |
| D. | 船过河的最短时间是一定的 |
 图是研究自感现象的电路图,两个电流表G1和G2的零点都在刻度中央,当电流从“+”接线柱流入时,指针向右偏,反之向左偏,在电键K接通的瞬间,G1指针向向右摆,G2指针向向右摆动(填“左”、“右”);K断开的瞬间,G1指针向向右摆,G2指针向向左摆动,两个电表的示数相等(填“相等”或“不相等”).
图是研究自感现象的电路图,两个电流表G1和G2的零点都在刻度中央,当电流从“+”接线柱流入时,指针向右偏,反之向左偏,在电键K接通的瞬间,G1指针向向右摆,G2指针向向右摆动(填“左”、“右”);K断开的瞬间,G1指针向向右摆,G2指针向向左摆动,两个电表的示数相等(填“相等”或“不相等”). 如图所示,质量mA=0.9kg的软木块放在粗糙的水平面上,木块与水平面的动摩擦因数为0.2.质量m0=0.1kg的子弹以速度v0=10m/s打入软木块,已知子弹与木块的摩擦因数为0.9,木块的长度为L=0.6m,求:
如图所示,质量mA=0.9kg的软木块放在粗糙的水平面上,木块与水平面的动摩擦因数为0.2.质量m0=0.1kg的子弹以速度v0=10m/s打入软木块,已知子弹与木块的摩擦因数为0.9,木块的长度为L=0.6m,求: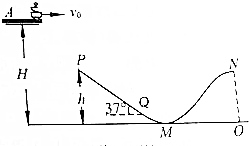 如图所示,A是高为H=5m的平台,与轨道PQMN在同一竖直平面上,PQMN依次为平滑连接的滑行轨道,其中PQ段与水平面成θ=37°,P端离地面高h=3.2m,QMN由半径为R1=10m的凹行圆弧轨道和平滑凸行轨道组成.其中M点为凹行圆弧轨道的最低点,N点为凸形轨道的最高点,N点附近轨道可看作圆心在O点半径为R2的圆弧轨道.已知滑板及运动员的总质量m=60kg,运动员从A点水平滑出,经P点切入轨道PQ(速度方向恰好沿PQ方向),经M点后从N点水平飞出.(运动过程中可把滑板及运动员视为质点,忽略摩擦阻力和空气阻力,sin37°=0.6)
如图所示,A是高为H=5m的平台,与轨道PQMN在同一竖直平面上,PQMN依次为平滑连接的滑行轨道,其中PQ段与水平面成θ=37°,P端离地面高h=3.2m,QMN由半径为R1=10m的凹行圆弧轨道和平滑凸行轨道组成.其中M点为凹行圆弧轨道的最低点,N点为凸形轨道的最高点,N点附近轨道可看作圆心在O点半径为R2的圆弧轨道.已知滑板及运动员的总质量m=60kg,运动员从A点水平滑出,经P点切入轨道PQ(速度方向恰好沿PQ方向),经M点后从N点水平飞出.(运动过程中可把滑板及运动员视为质点,忽略摩擦阻力和空气阻力,sin37°=0.6)