题目内容
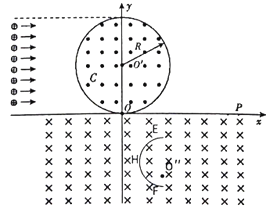
【题目】如图所示，在xOy平面内，以O'(O， R)为圆心、R为半径的圆内有垂直于平面向外的匀强磁场，x轴下方有足够大的垂直于平面向里的匀强磁场，两区域磁感应强度大小相等。在O"(
R，-R)处，放置一半径R=
的半圆弧形接收器EHF，EO"F与y轴平行，在圆形磁场的左侧0<y<2R的区间内均匀分布着质量为m、电荷量为+q的一簇带电粒子，当所有粒子均沿x轴正方向以速度v射人圆形磁场区域时，粒子偏转后都从O点进入x轴下方磁场，不计粒子重力、不考虑粒子间相互作用力，粒子离开磁场后不再回到磁场。求：
（1）磁场的磁感应强度B的大小；
（2）［-R，（
+1）R］处的粒子经磁场偏转后能否被接收器接收；
（3）打到接收器上的粒子占粒子总数的百分比。
【答案】（1）B=
；（2）不能；（3）50
【解析】
（1）粒子在上方磁场中的半径r=R时，粒子偏转后都从O点进入，由洛伦茨力充当向心力
qvB=m
解得磁场的磁感应强度B的大小为B=。
（2）［-R，（
+1）R］处的粒子经上方磁场偏转后与x轴负方向的角度
=
=
，
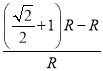=45°，粒子与x轴负方向成45°角进入下方磁场运动时，圆心在（R，-R）处，轨迹与接收器不相交，所以不能被接收器接受，如下图：
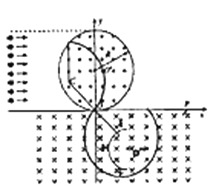
（3）当粒子运动轨迹与接收器在F点相内切时，由几何关系可知，运动轨迹的圆心恰好在E点，根据几何关系可知，粒子由O点进入时，粒子的速度方向与y轴负方向的夹角
=
=
，
=30°，粒子进入上方磁场G时的纵坐标
y1=R+R
=1.5R
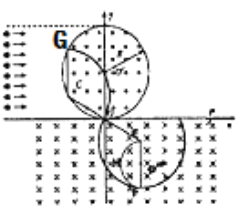
当粒子运动轨迹在E点与接收器相外切时，运动轨迹的圆心恰好在（R，
R）处，根据几何关系可知，粒子由O点进入磁场时粒子速度方向与x轴正方向的夹角
==，
=60°，粒子进入上方磁场I的纵坐标
y2=R- R
=0.5R
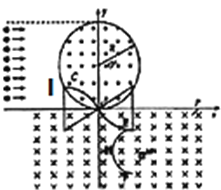
在上方磁场GI间射入的粒子能打到接收器上，LGI=y1-y2=R，占粒子总数的百分比
=
100=50。
答：（1）磁场的磁感应强度B=；（2）不能；（3）50
