��Ŀ����
4����ͼ��ʾ�����費�ƵĽ�������PQ��MNˮƽƽ�з��ã����ΪL�������P��M�˽ӵ�������Ϊn1��n2=1��2�������ѹ����ԭ��Ȧ���ˣ�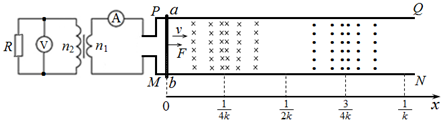 ��ѹ���ĸ���Ȧ������ֵΪR�ĵ��裮���������x��0�����д�ֱ����ƽ��Ĵų����ų��ĴŸ�Ӧǿ��B=B0sin2k��x��һ��ֵ���Ƶĵ����ab��ֱ����������뵼��Ӵ����ã���ʼʱ���������x=0������t=0ʱ���𣬵����ab����x���������F���������ٶ�Ϊv�������˶���������
��ѹ���ĸ���Ȧ������ֵΪR�ĵ��裮���������x��0�����д�ֱ����ƽ��Ĵų����ų��ĴŸ�Ӧǿ��B=B0sin2k��x��һ��ֵ���Ƶĵ����ab��ֱ����������뵼��Ӵ����ã���ʼʱ���������x=0������t=0ʱ���𣬵����ab����x���������F���������ٶ�Ϊv�������˶���������| A�� | �����ab�в����Ľ��������Ƶ��Ϊkv | |
| B�� | ������ѹ����ʾ��Ϊ2B0Lv | |
| C�� | ������������ʾ��Ϊ$\frac{{4{B_0}Lv}}{R}$ | |
| D�� | ��tʱ������F���Ĺ�Ϊ$\frac{{2B_0^2{L^2}{v^2}t}}{R}$ |
���� �����и�����ĸ�Ӧ�綯�ƹ�ʽ���õ���Ӧ�綯�Ƶı���ʽ�����ɵõ�Ƶ�ʣ����ԭ��Ȧ��ѹ����Чֵ���ɱ�ѹ���Ĺ�����⽻����ѹ����ʾ������ϱպϵ�·ŷķ���������Ӧ��������Чֵ�����ɵõ�������������ʾ������·�в����ĸ�Ӧ����Ϊ���������������Чֵ���R�������������Ӷ��õ�F���Ĺ���
��� �⣺A����tʱ��ab��������Ϊ x=vt
��Ӧ�綯�� e=BLv=B0Lvsin2k��v t
������Ľ�Ƶ��Ϊ��=2k��v
���������Ƶ��Ϊ f=$\frac{��}{2��}$=��v����A��ȷ��
B��ԭ��Ȧ���˵ĵ�ѹ U1=$\frac{{B}_{0}Lv}{\sqrt{2}}$
��$\frac{{U}_{1}}{{U}_{2}}$=$\frac{{n}_{1}}{{n}_{2}}$=$\frac{1}{2}$���ø���Ȧ���˵ĵ�ѹΪ U2=$\frac{2{B}_{0}Lv}{\sqrt{2}}$=$\sqrt{2}$B0Lv���ʽ�����ѹ����ʾ��Ϊ$\sqrt{2}$B0Lv����B����
C������Ȧ�е�����ЧֵΪ I2=$\frac{{U}_{2}}{R}$=$\frac{\sqrt{2}{B}_{0}Lv}{R}$
��$\frac{{I}_{2}}{{I}_{1}}$=$\frac{{n}_{1}}{{n}_{2}}$=$\frac{1}{2}$����ԭ��Ȧ�е�����ЧֵΪ I1=$\frac{2\sqrt{2}{B}_{0}Lv}{R}$�����Խ�����������ʾ��Ϊ$\frac{2\sqrt{2}{B}_{0}Lv}{R}$����C����
D����tʱ������F���Ĺ�����R������������Ϊ W=$\frac{{U}_{2}^{2}}{R}$t=$\frac{{2B_0^2{L^2}{v^2}t}}{R}$����D��ȷ��
��ѡ��AD��
���� �������Ĺؼ�֪�������������ĸ�Ӧ����Ϊ������������������ʱӦ���õ�ѹ����Чֵ�����������ֵ��

 ��У����ϵ�д�
��У����ϵ�д�| A�� | ٤���� | B�� | ������ | C�� | ţ�� | D�� | ���ĵ��� |
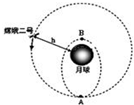 ��ͼ���ҹ�����ġ��϶���š����������ھ��������100km��Բ�ι���ϣ���A��ʱ����������Բ������У������������15km��B�����������㣬�����ж���ȷ���ǣ�������
��ͼ���ҹ�����ġ��϶���š����������ھ��������100km��Բ�ι���ϣ���A��ʱ����������Բ������У������������15km��B�����������㣬�����ж���ȷ���ǣ�������| A�� | ������Բ���������ʱ����ʧ��״̬�������������� | |
| B�� | ����Բ������˶�������С����Բ������˶������� | |
| C�� | ���Ǵ�Բ���������Բ���������ƶ� | |
| D�� | ��Բ�������ʱ��A��ļ��ٶȺ�����Բ�������ʱ��A��ļ��ٶȴ�С���� |
| A�� | ����������ֱ���˶� | B�� | �������ȱ��������˶� | ||
| C�� | ���������ȼ���ֱ���˶� | D�� | ���������ȼ���ֱ���˶� |
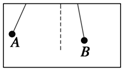 ��ͼ��ʾ��A��B�ֱ�Ϊ��������г��ʱ����IJ�ͬλ�ã����У�λ��AΪ����ڶ������λ�ã�����Ϊ���������ֱ�ߣ��������λ��Ϊ����������㣬������ڰڶ������У�������
��ͼ��ʾ��A��B�ֱ�Ϊ��������г��ʱ����IJ�ͬλ�ã����У�λ��AΪ����ڶ������λ�ã�����Ϊ���������ֱ�ߣ��������λ��Ϊ����������㣬������ڰڶ������У�������| A�� | ����λ��B��ʱ������� | |
| B�� | ����λ��A��ʱ������� | |
| C�� | ������λ��B�Ļ�е�ܵ�����λ��A�Ļ�е�� | |
| D�� | ������λ��B�Ļ�е�ܴ�����λ��A�Ļ�е�� |
| A�� | �����С�Ĵ�������ǵ��� | |
| B�� | Ԫ��ɾ���ָһ�����ӻ�һ������ | |
| C�� | �����������������ֹ���ɼ������ã�������ʹ�ù�ʽF=k$\frac{{{q_1}{q_2}}}{r^2}$ | |
| D�� | ����õ��������ɣ����۵�����Ƿ���ȣ�����֮��Ŀ�������Сһ����� |
| A�� | ���ĵ���ͨ��ʵ��������������G | |
| B�� | ţ���ܽ���������˶���������� | |
| C�� | ����˹̹������������������ | |
| D�� | �����ս�������������� |
| A�� | $\frac{1}{6}$mgR | B�� | $\frac{1}{8}$mgR | C�� | $\frac{1}{9}$mgR | D�� | $\frac{1}{14}$mgR |
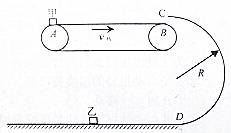 ��ͼ��ʾ������Ϊm��С�����������v��=5m/s���������˶��Ĵ��ʹ������Aλ�ã�������˶������ʹ��Ҷ�Bλ�ú��C����Բ�����߽���뾶R=0.2m����ֱ�⻬��Բ�ι������������͵�D����ˮƽ�⻬��������뾲ֹ��ˮƽ��������Ϊkm��С����ҷ���������ײ���ֲ�����ջ��������͵�Dʱ��ˮƽ�����ѹ��N=13.5mg�������봫������Ķ�Ħ��������=0.4��gȡ10m/s2������
��ͼ��ʾ������Ϊm��С�����������v��=5m/s���������˶��Ĵ��ʹ������Aλ�ã�������˶������ʹ��Ҷ�Bλ�ú��C����Բ�����߽���뾶R=0.2m����ֱ�⻬��Բ�ι������������͵�D����ˮƽ�⻬��������뾲ֹ��ˮƽ��������Ϊkm��С����ҷ���������ײ���ֲ�����ջ��������͵�Dʱ��ˮƽ�����ѹ��N=13.5mg�������봫������Ķ�Ħ��������=0.4��gȡ10m/s2������