题目内容
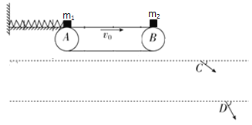
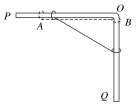
【题目】如图所示,质量为2m和m的两个弹性环A、B用不可伸长的、长为L的轻绳连接,分别套在水平细杆OP和竖直细杆OQ上,OP与OQ在O点用一小段圆弧杆平滑相连,且OQ足够长.初始时刻,将轻绳拉至水平位置伸直,然后释放两个小环,A环通过小段圆弧杆时速度大小保持不变,重力加速度为g,不计一切摩擦,试求:
(1)当B环下落![]() 时A球的速度大小;
时A球的速度大小;
(2)A环到达O点后再经过多长时间能够追上B环;
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)A与B下降的过程中系统的机械能守恒,先由速度的合成与分解求出A、B速度的关系,然后即可求出A、B在不同点的速度;
(2)根据匀变速直线运动的公式,结合位移关系即可求出A追上B的时间。
(1)当B环下落![]() 时绳子与水平方向之间的夹角满足sin α=
时绳子与水平方向之间的夹角满足sin α=![]() ,即α=30°
,即α=30°
由速度的合成与分解可知v绳=vAcos 30°=vBsin 30°
则vB=![]() =
=![]() vA
vA
B下降的过程中A与B组成的系统机械能守恒,有![]()
所以A环的速度vA= ![]()
(2)由于A到达O点时B的速度等于0,由机械能守恒,
![]() 2mvA′2=mgL,
2mvA′2=mgL,
解得vA′=![]()
环A过O点后做初速度为vA′、加速度为g的匀加速直线运动,B做自由落体运动;
当A追上B时,有vA′t+![]() gt2=L+
gt2=L+![]() gt2
gt2
解得t=![]()

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目