��Ŀ����
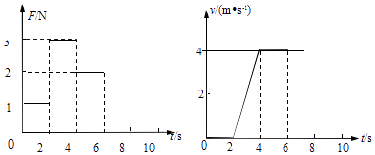
����Ŀ����Ǧ�=37���б����̶���ˮƽ�����ϣ�һ����������̶���б�涥�˵Ķ����֣�����һ��������Ϊml=1kg�����A���ӣ�������б��ƽ�У���һ��������Ϊm2=3kg�����B���ӣ���ʼʱ�����ְ�סA��ʹB���ھ�����H=0.6m������A��ֹ��б��ˣ���ͼ��ʾ�����ͷ�B������˺�A��б�������ϻ��е������룿����б���㹻���������нӴ�����Ħ�������Բ��ƣ�sin37��=0.6��cos37��=0.8��gȡ10m/s2��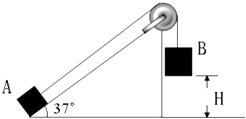
���𰸡��⣺��B���ʱ���ٶ�Ϊv��ϵͳ�Ļ�е���غ㣺
m2gH��m1gHsin��= ![]() ��m1+m2��v2��
��m1+m2��v2��
B��غ�A��vΪ���ٶ���б���ȼ�������������б���������ľ���ΪS��
�ɶ��ܶ����ã���m1gSsin��=0�� ![]() mv2��
mv2��
����m����б�滬�е������룺L=h+S ��
�ɢ٢ڢ۴������ݵã�L=1.2m
������A����б�滬�е���������1.2m
��������A��B��ʼ�˶���B�ŵع����У�����ϵͳ�����������������ϵͳ�Ļ�е���غ㣬���û�е���غ㶨��������ǵ��ٶȣ�
B�ŵغ�A��б�����ȼ����˶������ٶȼ�Ϊ��ʱ��A����б�滬�еľ������
�����㾫�������ڱ��⿼��Ļ�е���غ㼰�������ͻ�е���ۺ�Ӧ�ã���Ҫ�˽���ֻ���������͵��ɵ����������������£����嶯�ܺ��������ܣ����������ܣ������ת��������е�ܵ��������ֲ��䣻ϵͳ��̬���ܻ�е��E 1 ����ĩ̬���ܻ�е��E 2 ����E1 =E2��ϵͳ���ٵ����������ܦ�E P�� ����ϵͳ���ӵ��ܶ��ܦ�E K�� ������E P�� =��E K������ϵͳֻ��A��

 ��У����ϵ�д�
��У����ϵ�д�