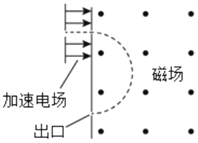
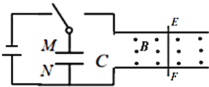
题目内容
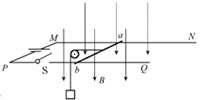
【题目】实验室中有一直角三角形玻璃砖，如图所示为该玻璃砖的截面ABC，其中，
,D、E是斜边上的三等分点，斜边AC长为3a，让玻璃砖竖直放置，在底边BA的延长线上有一点光源S，光源S与A的距离为a。光源S发出的两束不同频率的单色光1、2分别照射到斜边上的E、D点，经斜边折射后进入玻璃砖中的光线的平行于底边AB，然后在BC边第一次射出。已知光在真空中的传播速度为c。求：
（1）光束1在玻璃砖中传播的速度；
（2）光束2第一次在玻璃砖中传播的时间；
【答案】（i）
（ii）
【解析】
解(1)由题知光路如图所示，由几何关系得
，
由折射定律得：
光束1在玻璃砖中传播的速度为：
(2)设
，则
由正弦定理有：
解得：
由三角函数知识知：
由几何关系得：
由折射定律知：
光束2在玻璃砖中传播的速度
光束2第一次在玻璃砖中传播的距离为
光束2第一次在玻璃砖中传播时间为
练习册系列答案
口算能手系列答案
相关题目
