题目内容
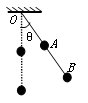
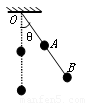
 长为2L的轻杆从中点处弯成互相垂直的两部分,搭在光滑水平轴O上,如图所示,A端固定质量为M小球,B端固定质量为m的小球,在OB中点也固定一质量为m小球.现在将OA由水平静止释放,当OA竖直时(OB水平)开始回转,不计一切阻力,则M、m关系是( )
长为2L的轻杆从中点处弯成互相垂直的两部分,搭在光滑水平轴O上,如图所示,A端固定质量为M小球,B端固定质量为m的小球,在OB中点也固定一质量为m小球.现在将OA由水平静止释放,当OA竖直时(OB水平)开始回转,不计一切阻力,则M、m关系是( )分析:将OA由水平静止释放,当OA竖直时(OB水平)开始回转,说明当OA竖直时M球的速度为零,OB水平时,两个m球速度也为零,系统在运动过程中,只有重力做功,机械能守恒,根据机械能守恒定律列式即可求解.
解答:解:当OA竖直时(OB水平)时,三个球的速度都为零,系统运动过程中,只有重力做功,机械能守恒,
根据机械能守恒定律得:
MgL=mg
+mgL
解得:M=
m
故选:D.
根据机械能守恒定律得:
MgL=mg
| L |
| 2 |
解得:M=
| 3 |
| 2 |
故选:D.
点评:本题主要考查了机械能守恒定律的直接应用,难度不大,属于基础题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
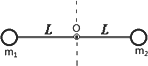
 (2)若在如图所示的位置时,轻杆对A球的作用力恰好为零,B球从杆上脱落,求:
(2)若在如图所示的位置时,轻杆对A球的作用力恰好为零,B球从杆上脱落,求: