题目内容
7.一摆长为1m的单摆在地球表面做简谐运动,若取π2=g,(1)求该单摆在地球表面振动的周期;
(2)将该单摆移到半径是地球半径4倍,平均密度和地球相等的某星球表面,求其振动周期变为多少?
分析 (1)据单摆的振动周期公式T=2π$\sqrt{\frac{L}{g}}$求解.
(2)据星球表面重力近似等于万有引力、星球的体积和质量、体积与密度关系式列式;再利用单摆的振动周期公式求解.
解答 解:单摆的振动周期公式T=2π$\sqrt{\frac{L}{g}}$=2$π\sqrt{\frac{1}{{π}^{2}}}$=2s
(2)据星球表面重力近似等于万有引力,所以$\frac{GMm}{{R}^{2}}=mg$
又因为:M=ρV
V=$\frac{4π{R}^{3}}{3}$
单摆的振动周期公式T=2π$\sqrt{\frac{L}{g}}$
联立以上解得:T=1s
答:(1)求该单摆在地球表面振动的周期2s;
(2)将该单摆移到半径是地球半径4倍,平均密度和地球相等的某星球表面,求其振动周期变为1s.
点评 解本题需要具备以下知识:单摆的振动周期公式T=2π$\sqrt{\frac{L}{g}}$、星球表面重力近似等于万有引力、体积和质量公式,此题综合性较强.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
9. 如图所示,为工厂中的行车示意图,设钢丝长4m,用它吊着质量为20kg的铸件,行车以2m/s的速度匀速行驶,当行车突然刹车停止运动时,钢丝中受到的拉力大小为(g=10m/s2)( )
如图所示,为工厂中的行车示意图,设钢丝长4m,用它吊着质量为20kg的铸件,行车以2m/s的速度匀速行驶,当行车突然刹车停止运动时,钢丝中受到的拉力大小为(g=10m/s2)( )
 如图所示,为工厂中的行车示意图,设钢丝长4m,用它吊着质量为20kg的铸件,行车以2m/s的速度匀速行驶,当行车突然刹车停止运动时,钢丝中受到的拉力大小为(g=10m/s2)( )
如图所示,为工厂中的行车示意图,设钢丝长4m,用它吊着质量为20kg的铸件,行车以2m/s的速度匀速行驶,当行车突然刹车停止运动时,钢丝中受到的拉力大小为(g=10m/s2)( )| A. | 250N | B. | 220N | C. | 200N | D. | 180N |
10.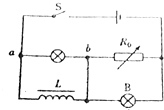 如图所示,A,B是两个相同的小灯泡,电阻均为R,R0是电阻箱,L是自感系数较大的线圈,当S闭合调节R0的阻值使电路稳定时,A,B亮度相同,则在开关S断开时,下列说法中正确的是( )
如图所示,A,B是两个相同的小灯泡,电阻均为R,R0是电阻箱,L是自感系数较大的线圈,当S闭合调节R0的阻值使电路稳定时,A,B亮度相同,则在开关S断开时,下列说法中正确的是( )
 如图所示,A,B是两个相同的小灯泡,电阻均为R,R0是电阻箱,L是自感系数较大的线圈,当S闭合调节R0的阻值使电路稳定时,A,B亮度相同,则在开关S断开时,下列说法中正确的是( )
如图所示,A,B是两个相同的小灯泡,电阻均为R,R0是电阻箱,L是自感系数较大的线圈,当S闭合调节R0的阻值使电路稳定时,A,B亮度相同,则在开关S断开时,下列说法中正确的是( )| A. | B灯立即熄灭 | |
| B. | A灯一定将比原来更亮一些后再熄灭 | |
| C. | 若R0=R,则A灯立即熄灭 | |
| D. | 有电流通过A灯,方向为b→a |
15. 如图所示,平行板MN间为匀强电场.在垂直匀强电场方向上存在着匀强磁场,带电粒子(重力不计)沿两极板中央垂直电场及磁场的方向射入此区域;粒子能否沿此方向做匀速直线运动,与以下条件中哪些相关( )
如图所示,平行板MN间为匀强电场.在垂直匀强电场方向上存在着匀强磁场,带电粒子(重力不计)沿两极板中央垂直电场及磁场的方向射入此区域;粒子能否沿此方向做匀速直线运动,与以下条件中哪些相关( )
 如图所示,平行板MN间为匀强电场.在垂直匀强电场方向上存在着匀强磁场,带电粒子(重力不计)沿两极板中央垂直电场及磁场的方向射入此区域;粒子能否沿此方向做匀速直线运动,与以下条件中哪些相关( )
如图所示,平行板MN间为匀强电场.在垂直匀强电场方向上存在着匀强磁场,带电粒子(重力不计)沿两极板中央垂直电场及磁场的方向射入此区域;粒子能否沿此方向做匀速直线运动,与以下条件中哪些相关( )| A. | 与带电粒子所带电性(正负)有关 | B. | 与带电粒子所带电量多少有关 | ||
| C. | 与带电粒子质量大小有关 | D. | 与带电粒子入射的初速度有关 |
12.两物体在不同高度自由下落,同时落地,第一个物体下落时间为t,第二个物体下落时间为$\frac{t}{2}$,当第二个物体开始下落时,甲乙两物体相对地面的高度之比是( )
| A. | 2:1 | B. | 3:1 | C. | 4:1 | D. | 4:3 |
19. 如图所示,在静止的平板车上放置一个质量为10kg的物体A,它被拴在一个水平拉伸的弹簧一端(弹簧另一端固定),且处于静止状态,此时弹簧的拉力为5N.若平板车从静止开始向右做加速运动,且加速度逐渐增大到1m/s2.则( )
如图所示,在静止的平板车上放置一个质量为10kg的物体A,它被拴在一个水平拉伸的弹簧一端(弹簧另一端固定),且处于静止状态,此时弹簧的拉力为5N.若平板车从静止开始向右做加速运动,且加速度逐渐增大到1m/s2.则( )
 如图所示,在静止的平板车上放置一个质量为10kg的物体A,它被拴在一个水平拉伸的弹簧一端(弹簧另一端固定),且处于静止状态,此时弹簧的拉力为5N.若平板车从静止开始向右做加速运动,且加速度逐渐增大到1m/s2.则( )
如图所示,在静止的平板车上放置一个质量为10kg的物体A,它被拴在一个水平拉伸的弹簧一端(弹簧另一端固定),且处于静止状态,此时弹簧的拉力为5N.若平板车从静止开始向右做加速运动,且加速度逐渐增大到1m/s2.则( )| A. | 物体A相对于车向左运动 | B. | 物体A受到的弹簧的拉力逐渐增大 | ||
| C. | 物体A受到的摩擦力逐渐减小 | D. | 物体A受到的摩擦力先减小后增大 |
16.以下说法错误的是( )
| A. | 自由下落的物体因完全失重,所以它对地球没有反作用力 | |
| B. | 两叠放着的木块A、B一起在光滑斜面上自由下滑而没有相对滑动,A、B间没有相互的摩擦力 | |
| C. | 物体受到的一对平衡力中撤去其中一个力,另一个力也同时消失 | |
| D. | 作用力和反作用力可以是不同性质的力 |
17.某种型号手机充电器中的变压器可认为是理想变压器,它的原、副线圈匝数比为50:1,若在原线圈上加有交流电压220V,则在副线圈上可获得电压( )
| A. | 4.4 V | B. | 220 V | C. | 11000V | D. | 1V |