题目内容
杂技演员在进行“顶杆”表演时，用的是一根质量可忽略不计的长竹竿，质量为30kg的演员自杆顶由静止开始下滑，滑到杆底时速度正好为零．已知竹竿底部与下面顶杆人肩部之间有一传感器，传感器显示顶杆人肩部的受力情况如图所示，取g=10m/s2．求：（1）杆上的人下滑过程中的最大速度；
（2）竹竿的长度．
【答案】分析：（1）以人为研究对象，人加速下滑过程中受重力mg和杆对人的作用力F1，由题图可知，人加速下滑过程中杆对人的作用力F1为180 N．由牛顿第二定律可以求得加速度，1s末人的速度达到最大，根据速度时间公式即可求解；
（2）先求出加速下降的位移，再根据动能定理求出减速下降的位移，两段位移之和即为杆的长度．
解答：解：（1）以人为研究对象，人加速下滑过程中受重力mg和杆对人的作用力F1，由题图可知，人加速下滑过程中杆对人的作用力F1为180 N．
由牛顿第二定律得
mg-F1=ma，
则a=4 m/s2．
1s末人的速度达到最大，则v=at1=4 m/s．
（2）加速下降时位移为：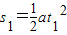
=2 m．
减速下降时，由动能定理得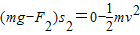
，
代入数据解得s2=4m，
杆的长度s=s1+s2=6m．
答：（1）杆上的人下滑过程中的最大速度为4m/s；
（2）竹竿的长度为6m．
点评：本题主要考查了牛顿第二定律及运动学基本公式的直接应用，要求同学们能根据图象得出有效信息，能根据受力情况判断运动情况，难度适中．
（2）先求出加速下降的位移，再根据动能定理求出减速下降的位移，两段位移之和即为杆的长度．
解答：解：（1）以人为研究对象，人加速下滑过程中受重力mg和杆对人的作用力F1，由题图可知，人加速下滑过程中杆对人的作用力F1为180 N．
由牛顿第二定律得
mg-F1=ma，
则a=4 m/s2．
1s末人的速度达到最大，则v=at1=4 m/s．
（2）加速下降时位移为：
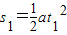=2 m．减速下降时，由动能定理得
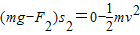，代入数据解得s2=4m，
杆的长度s=s1+s2=6m．
答：（1）杆上的人下滑过程中的最大速度为4m/s；
（2）竹竿的长度为6m．
点评：本题主要考查了牛顿第二定律及运动学基本公式的直接应用，要求同学们能根据图象得出有效信息，能根据受力情况判断运动情况，难度适中．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
杂技演员在进行“顶杆”表演 时，用的是一根质量为m=10kg的长竹竿．质量为M=30kg的演员自竹竿顶部由静止开始下滑，滑到竿底时速度恰好为零．已知竿底部与下面顶杆人肩部之间有一力传感器．竹竿处于静止状态，传感器显示顶杆人肩部的受力情况如图所示，g=10m/s2．求：