题目内容
10.如图(a)所示,在光滑绝缘水平面的AB区域内存在水平向右的电场,场强E随时间的变化如图(b)所示.不带电的绝缘小球P2静止在O点,t=0时,带正电的小球P1以速度v0从A点进入AB区域,随后与P2发生正碰后反弹,反弹速度大小是碰前的$\frac{2}{3}$倍,P1的质量为m1,带电量为q,P2的质量m2=5m1,A、O间距为L0,O、B间距$L=\frac{4}{3}{L_0}$(已知$\frac{q{E}_{0}}{{m}_{1}}$=$\frac{{2v}_{0}^{2}}{3{L}_{0}}$,T=$\frac{{L}_{0}}{{v}_{0}}$.)求:
(1)碰撞后小球P1向左运动的最大距离
(2)碰撞后小球P1向左运动所需时间;
(3)讨论两球能否在OB区间内再次发生碰撞.
分析 (1)(2)P1从A到O的过程是匀速直线运动,知道了AO的距离和P1速度,可求出P1从A到O所用的时间t,当P1到达O点与P2碰撞,碰撞过程中符合动量守恒.又因条件中有T=$\frac{{L}_{0}}{{v}_{0}}$,故碰后P1开始受到电场力的作用,向左做匀减速运动,用运动学公式和牛顿第二定律可求出P1向做运动的最大位移和所需时间.
(3)讨论两球在OB区域能否再次发生碰撞,就是判断从第一次碰撞开始,在4T的时间内,P1能否追上P2,此问利用假设法解答,假设能碰撞,可判断此过程中两球的位移相等.应用运动学公式验证假设成立.
解答 解:(1)小球P1到达O点的时间T=$\frac{{L}_{0}}{{v}_{0}}$,与P2碰撞时,电场刚好由零变为E0,碰撞后,P1的速度:v1=$\frac{2}{3}$v0,在电场中,P1的加速度是:a=$\frac{q{E}_{0}}{{m}_{1}}$,
在t1时间内,有电场,P1做匀减速运动P1向左运动的最大距离为:s=$\frac{{v}_{1}^{2}}{2a}$=$\frac{1}{3}$L0;
(2)由动能定理:$q{E_0}s=\frac{1}{2}mv_1^2=\frac{1}{2}m{(\frac{2}{3}v_0^{\;})^2}$s,
由动量定理:qE0t=mv1,
解得:t=T;
(3)系统动量守恒,以向右为正方向,由动量守恒定律得:m1v0=m1v1+m2v2
解得P2的速度:v2=$\frac{1}{3}$v0,
P2从O点运动到B点所需时间:t2=$\frac{L}{{v}_{2}}$=4T,
在t2时间内,一直存在电场,则P1的位移:x1=v1t2+$\frac{1}{2}$at22=2L,
由于x1>L,故在OB之间P1与P2能再次碰撞;
答:(1)碰撞后小球P1向左运动的最大距离为$\frac{1}{3}$L0;
(2)碰撞后小球P1向左运动所需时间为T;
(3)两球能否在OB区间内能再次发生碰撞.
点评 判断两球在O点碰撞后P1开始受电场力的作用是解决本题关键之一,碰撞过程动量守恒.分析判断P1碰撞后在电场力的作用下如何运动和追击P2是解决本题的关键之二,还要判断在追击过程中,P1受到的电场力是否发生变化.教具追击与相遇问题的关键是寻找相关联的物理量,此题中位移关系成了相关联的量.此题电场强度E随时间的变化改成到3T时电场消失,第二问又应如何解答呢?

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案(1)需要的器材有:打点计时器、长木板、复写纸片、6v低压交变电源、纸带、刻度尺、导线.
(2)下列说法正确的是B
A.拖动纸带的同时,闭合电源开关
B.先闭合电源开关,让打点计时器正常工作时,拖动纸带
C.纸带上的打点密集说明纸带运动速度较大
D.利用打出的纸带可以准确的求出打下某些点时纸带运动的瞬时速度
(3)某同学拖动纸带运动,打点计时器在纸带上打出一系列点,处理时每隔1个点取一个记数点,标上字母A、B、C、D、E、F.
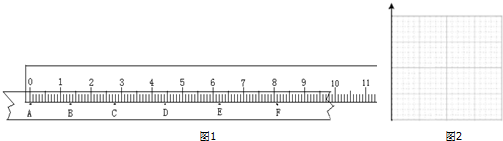
如图1所示,某同学用mm刻度尺进行测量,请帮忙读出B、C、D、E、F在刻度尺上的位置,填到表中:
| 计数点 | B | C | D | E | F |
| 单位(cm) |
(4)若认为一段时间中间时刻的瞬时速度就是这段时间内的平均速度,则打点计时器打下C点时小车的速度VC=4.388m/s,小车从C点运动D点过程中的加速度a=1.00m/s2.
(5)在如图2所给坐标纸上建好坐标,作出纸带运动的打下B至E点的速度-时间图象(即v-t图象)(从打下A点开始计时).
 如图所示,质量相同的木块A、B用轻质弹簧连接,静止在光滑的水平面上,此时弹簧处于自然状态.现用水平恒力F推A,则从力F开始作用到弹簧第一次被压缩到最短的过程中( )
如图所示,质量相同的木块A、B用轻质弹簧连接,静止在光滑的水平面上,此时弹簧处于自然状态.现用水平恒力F推A,则从力F开始作用到弹簧第一次被压缩到最短的过程中( )| A. | 弹簧压缩到最短时,两物块的速度相同 | |
| B. | 弹簧压缩到最短时,两物块的加速度相同 | |
| C. | 两木块速度相同时,加速度aA>aB | |
| D. | 两木块加速度相同时,速度vA>vB |
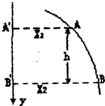 某同学在做平抛实验时,未记下槽的末端点的位置,记下了重锤线方向y,只描出图所示的一段轨迹,轨迹上A、B两点到Y轴的距离分别为xl、x2,A、B两点的竖直距离为h,则小球平抛速度v0=$\sqrt{\frac{g}{2h}({{x}_{2}}^{2}-{{x}_{1}}^{2})}$.
某同学在做平抛实验时,未记下槽的末端点的位置,记下了重锤线方向y,只描出图所示的一段轨迹,轨迹上A、B两点到Y轴的距离分别为xl、x2,A、B两点的竖直距离为h,则小球平抛速度v0=$\sqrt{\frac{g}{2h}({{x}_{2}}^{2}-{{x}_{1}}^{2})}$. 如图所示,a为一电荷量为q=1.0×10-5C的正点电荷,b为一原来不带电的导体,c、d为导体b内的两点,这两点到点电荷a的距离都等于10cm,当导体b处于静电平衡状态时,导体上的感应电荷在c点和d点产生的电场强度大小分别为Ec=9×106N/C,Ed=9×106N/C.请在图中画出感应电荷在c、d两点产生的电场强度的方向.
如图所示,a为一电荷量为q=1.0×10-5C的正点电荷,b为一原来不带电的导体,c、d为导体b内的两点,这两点到点电荷a的距离都等于10cm,当导体b处于静电平衡状态时,导体上的感应电荷在c点和d点产生的电场强度大小分别为Ec=9×106N/C,Ed=9×106N/C.请在图中画出感应电荷在c、d两点产生的电场强度的方向.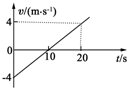 一质点做直线运动,t=0时,位于坐标原点,如图为质点做直线运动的速度-时间图象.由图可知:
一质点做直线运动,t=0时,位于坐标原点,如图为质点做直线运动的速度-时间图象.由图可知: 某同学在做研究平抛物体运动规律的实验时得到了如图所示的小球的运动轨迹,A、B、C三点的位置在运动轨迹上已标出.其中A点的坐标为(0,0),g=10m/s2,则
某同学在做研究平抛物体运动规律的实验时得到了如图所示的小球的运动轨迹,A、B、C三点的位置在运动轨迹上已标出.其中A点的坐标为(0,0),g=10m/s2,则