题目内容

【题目】如图所示，在动摩擦因数μ＝0.2的水平面上有一个质量m＝1kg的小球，小球分别与劲度系数为100N/m的水平轻弹簧及与竖直方向成θ＝45°角的不可伸长的轻绳一端相连，此时小球处于静止状态，且水平面对小球的弹力恰好为零．在剪断轻绳的瞬间(g取10m/s2，滑动摩擦力等于最大静摩擦力)，下列说法中正确的是

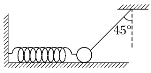
A. 小球受到地面的弹力仍然为零B. 小球的加速度方向向左，且a＝8m/s2

C. 小球的加速度方向向左，且a＝10m/s2D. 此时弹簧的伸长量为0.1m

【答案】BD

【解析】

剪断细线的瞬间,弹簧的弹力不变,对小球受力分析,确定小球的受力个数,根据牛顿第二定律求出瞬间的加速度大小.剪断弹簧的瞬间,因为绳子的作用力可以发生突变,小球瞬间所受的合力为零.

A．在剪断轻绳前,小球受重力、绳子的拉力以及弹簧的弹力处于平衡,根据共点力平衡得,弹簧的弹力: ， 剪断轻绳的瞬间,弹簧的弹力仍然为10N,小球此时受重力、支持力、弹簧弹力和摩擦力四个力作用，故A错；

BC．小球所受的最大静摩擦力为: ，所以小球有向左的加速度 ，故B对；C错；

D．剪断轻绳的瞬间,弹簧的弹力仍然为10N，所以 ，故D对；

故选BD

练习册系列答案
相关题目

【题目】如图所示，电流表A1(0～3 A)和A2(0～0.6 A)是由两个相同的灵敏电流计改装而成，现将这两个电流表并联后接入电路中。闭合开关S，调节滑动变阻器，下列说法正确的是(　　)

A. A1的读数小于A2的读数

B. A1的读数大于A2的读数

C. A1、A2的指针偏转角度之比为5∶1

D. A1、A2的指针偏转角度之比为1∶1

【题目】如图，海王星绕太阳沿椭圆轨道运动，P为近日点，Q为远日点，M，N为轨道短轴的两个端点，运行的周期为,若只考虑海王星和太阳之间的相互作用，则海王星在从P经过M、Q到N的运动过程中( )

A. 从P到M所用的时间等于

B. 从Q到N阶段，机械能逐渐变大

C. 从P到Q阶段，速率逐渐变大

D. 从M到N阶段，万有引力对它先做负功后做正功

【题目】如图所示，“嫦娥一号”卫星在飞向月球的过程中，经“地月转移轨道”到达近月点，为了被月球捕获成为月球的卫星，需要在点进行制动（减速）．制动之后进入轨道Ⅲ，随后在点再经过两次制动，最终进入环绕月球的圆形轨道Ⅰ．已知“嫦娥一号卫星”在轨道Ⅰ上运动时，卫星距离月球的高度为，月球的质量，朋球的，万有引力恒量为．忽略月球自转，求：

（）“嫦娥一号”在点的加速度．

（）“嫦娥一号”在轨道Ⅰ上绕月球做圆周运动的线速度．

（）若规定两质点相距无际远时引力势能为零，则质量分别为、的两个质点相距为时的引力势能，式中为引力常量．为使“嫦娥一号”卫星在点进行第一次制动后能成为月球的卫星，同时在随后的运动过程其高度都不小于轨道Ⅰ的高度，试计算卫星第一次制动后的速度大小应满足什么条件．

【题目】在“探究加速度与力、质量的关系”试验中：

(1)以下实验操作，正确的是_____________。

A．平衡摩擦力时，应将空砝码盘用细线跨过定滑轮系在小车上，让细线与长木板平行

B．平衡摩擦力时，应将纸带连接在小车上并穿过打点计时器

C．每次改变小车质量时，不需要重新平衡摩擦力

D．实验时，应先释放小车，再接通电源

(2)为了探究小车（包括里面所装钩码）总质量M一定时，加速度a与合力F的定量关系，需要在砝码盘里面添加砝码来改变小车所受到的合力．砝码质量m和小车总质量M分别选取下列四组值：

A．M=500g，m分别为50g、70g、100g、125g

B．M=500g，m分别为20g、30g、40g、50g

C．M=200g，m分别为50g、70g、100g、125g

D．M=200g，m分别为30g、40g、50g、60g

若其它操作都正确，那么应该选用_________组值（选填字母代号）进行实验时的实验误差较小．

(3)下图是实验中得到的一条已打点的纸带，纸带上的A、B、C、D、E、F、G均为相邻计数点，已知打点计时器的打点周期为0.02s，相邻两个计数点之间还有4个计时点未画出，相邻计数点之间的距离已标注在图上，则小车运动的加速度大小a=____m/s2，打C点时的速度大小vC=____m/s．（以上结果都保留2位有效数字）．

(4)某学生在平衡摩擦力时，使得长木板倾角偏大。他所得到的a-F关系是图中的哪根图线？（图中a是小车的加速度，F是细线作用于小车的拉力）。答：________________。

A、 B、

C、 D、

【题目】在地表附近有一竖直向下匀强电场E，一带电油滴以某初速度从a处运动到b处，其运动轨迹如图中曲线所示，不计空气阻力，此过程中油滴运动情况描述正确的是( )

A. 油滴在做变加速曲线运动

B. 油滴在做速度大小不变的曲线运动

C. 动能和电势能之和减小

D. 油滴的轨迹为椭圆的一部分

【题目】在图中所示的四种典型电场的情况中，电场中、两点的电场强度和电势都相等的是（ ）

A. 图（甲）中平行板电容器带电荷，极板间除边缘附近处的任意两点、

B. 图（乙）中两个等量异号点电荷的连线上，与连线中点等距的任意两点、

C. 图（丙）中离点电荷等距的任意两点、

D. 图（丁）中两个等量同号点电荷的连线的中垂线上,与连线中点等距的任意两点、

【题目】如图所示，长l=1m的轻质细绳上端固定，下端连接一个可视为质点的带电小球，小球静止在水平向右的匀强电场中，绳与竖直方向的夹角θ=37°．已知小球所带电荷量q=1.0×10﹣6 C，匀强电场的场强E=3.0×103 N/C，取重力加速度g=10m/s2，sin 37°=0.6，cos 37°=0.8．求：

（1）小球所受电场力F的大小．

（2）小球的质量m．

（3）将电场撤去，小球回到最低点时速度v的大小．

【题目】在竖直平面内，橡皮条一端固定在G点，另一端挂一小圆环，现用两个弹簧测力计拉动小圆环到O点，小圆环受到作用力F1、F2和橡皮条的拉力F0，如图所示.

(1)此时要记录下拉力F1、F2的大小，并在白纸上记录__________，以及O点的位置.

(2)实验中，不必要的是____________

A．用弹簧测力计测出小圆环的重力

B．弹簧测力计在使用前应校零

C．撤去F1、F2，改用一个力拉小圆环，仍使它处于O点

D.用两个弹簧测力计拉动小圆环时，要保持两弹簧测力计相互垂直

(3)图中F是用一个弹簧测力计拉小圆环时，在白纸上根据实验纠果画出的图示。F与F中，方向一定沿GO方向的是___________.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网