题目内容
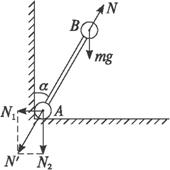
如图4-2-17所示是一同学荡秋千的示意图.人最初直立静止地站在B点，绳与竖直方向成θ角，人的重心到悬点O的距离为L1.从B点向最低点A摆动的过程中，人由直立状态自然下蹲，在最低点A人下蹲状态时的重心到悬点O的距离为L2.到最低点后人又由下蹲状态突然变成直立状态且保持直立状态不变，直到摆向另一方的最高点C（设人的质量为m，踏板质量不计，任何阻力不计）.求：
图4-2-17
（1）当人刚摆到最低点A且处于下蹲状态时，绳子中的拉力为多少?
（2）人保持直立状态到达另一方最高点C时，绳子与竖直方向的夹角α为多大?（用反三角函数表示）
思路点拨：该题是动能定理和能量守恒及圆周运动的综合应用题.
解析：（1）人由B摆到A的过程中，设在A点时人的速度为v，由动能定理知：
mg（L2-L1cosθ）=
mv2 ①
在最低点A时，设绳子的拉力为FT，据牛顿第二定律F=ma得FT-mg=
②
联立①②式解得：
FT=mg（3-
cosθ）.
（2）人保持直立状态由A摆到C的过程由动能定理知：
mv2=mg（L1-L1cosα） ③
联立①③式解得α=arccos（1+cosθ-
）.
答案： （1）mg（3-
cosθ）
（2）arccos（1+cosθ-
）
练习册系列答案
相关题目
）时，求： 
