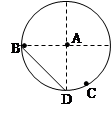题目内容
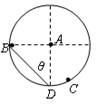
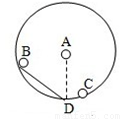
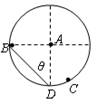
如图所示,将小球甲、乙、丙(都可视为质点)分别从A、B、C三点由静止同时释放,最后都到达竖直面内圆弧的最低点D。其中甲从圆心A出发做自由落体运动,乙沿底端在D点的该圆的一根弦轨道从弦的上端开始自由下滑,丙从圆弧轨道上很靠近D的某一位置开始沿圆弧自由下滑。三小球的初速度都是零,忽略一切摩擦阻力,下列说法中正确的是

- A.甲球最先到达D点,乙球最后到达D点
- B.甲球最先到达D点,丙球最后到达D点
- C.丙球最先到达D点,乙球最后到达D点
- D.甲球最先到达D点,但无法判断哪个最后到达D点
A
试题分析:A点,AD距离为r,加速度为g,时间t1= ;
;
B点,设∠ADB=θ,由几何关系:BD距离为2rcosθ,加速度为gcosθ,时间t2=2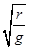 ;
;
C点,简谐振动,周期T=2π![]() ,时间t3=
,时间t3=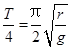 ;
;
明显t2>t3>t1,故A正确。
考点:本题考查牛顿运动定律、自由落体运动、简谐运动。
试题分析:A点,AD距离为r,加速度为g,时间t1=
 ;
;B点,设∠ADB=θ,由几何关系:BD距离为2rcosθ,加速度为gcosθ,时间t2=2
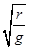 ;
;C点,简谐振动,周期T=2π
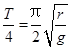 ;
;明显t2>t3>t1,故A正确。
考点:本题考查牛顿运动定律、自由落体运动、简谐运动。

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
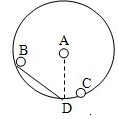 如图所示,将小球甲、乙、丙(都可视为质点)分别从A、B、C三点由静止同时释放,最后都到达竖直面内圆弧的最低点D,其中甲是从圆心A出发做自由落体运动,乙沿弦轨道从一端B到达另一端D,丙沿圆弧轨道从C点运动到D,且C点很靠近D点.如果忽略一切摩擦阻力,那么下列判断正确的是( )
如图所示,将小球甲、乙、丙(都可视为质点)分别从A、B、C三点由静止同时释放,最后都到达竖直面内圆弧的最低点D,其中甲是从圆心A出发做自由落体运动,乙沿弦轨道从一端B到达另一端D,丙沿圆弧轨道从C点运动到D,且C点很靠近D点.如果忽略一切摩擦阻力,那么下列判断正确的是( )