题目内容
如图,游乐场中,从高处A到水面B处有两条长度相同的光滑轨道。甲、乙两小孩沿不同轨道同时从A处自由滑向B处,下列说法正确的有

- A.甲的切向加速度始终比乙的大
- B.甲、乙在同一高度的速度大小相等
- C.甲、乙在同一时刻总能到达同一高度
- D.甲比乙先到达B处
BD
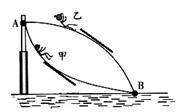
试题分析:物体沿光滑轨道下滑由牛顿第二定律得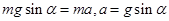 ,甲轨道与水平面的夹角减小,乙轨道与水平面的夹角增大,如图所示位置的夹角相等,该位置两轨道的加速度相等,此位置之前
,甲轨道与水平面的夹角减小,乙轨道与水平面的夹角增大,如图所示位置的夹角相等,该位置两轨道的加速度相等,此位置之前 ,此位置之后
,此位置之后 所以A选项错误;由机械能守恒
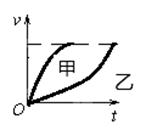
所以A选项错误;由机械能守恒 ,当h相同时速度大小相同,B选项正确;由v-t图象甲、乙在不能在同时刻到达同一高度,甲先到达B点,所以C选项错误,D选项正确。
,当h相同时速度大小相同,B选项正确;由v-t图象甲、乙在不能在同时刻到达同一高度,甲先到达B点,所以C选项错误,D选项正确。
考点:牛顿第二定律 机械能守恒定律 v-t图象的意义


试题分析:物体沿光滑轨道下滑由牛顿第二定律得
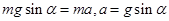 ,甲轨道与水平面的夹角减小,乙轨道与水平面的夹角增大,如图所示位置的夹角相等,该位置两轨道的加速度相等,此位置之前
,甲轨道与水平面的夹角减小,乙轨道与水平面的夹角增大,如图所示位置的夹角相等,该位置两轨道的加速度相等,此位置之前 ,此位置之后
,此位置之后 所以A选项错误;由机械能守恒
所以A选项错误;由机械能守恒 ,当h相同时速度大小相同,B选项正确;由v-t图象甲、乙在不能在同时刻到达同一高度,甲先到达B点,所以C选项错误,D选项正确。
,当h相同时速度大小相同,B选项正确;由v-t图象甲、乙在不能在同时刻到达同一高度,甲先到达B点,所以C选项错误,D选项正确。考点:牛顿第二定律 机械能守恒定律 v-t图象的意义

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 某游乐场开发了一个名为“翻天滚地”的游乐项目.原理图如图所示:一个
某游乐场开发了一个名为“翻天滚地”的游乐项目.原理图如图所示:一个| 3 |
| 4 |
A、要使球能从C点射出后能打到垫子上,则球经过C点时的速度至少为
| ||
| B、球从A到B的过程中重力的功率先减小后增大 | ||
C、若球从C点射出后恰好能打到垫子的M端,则球经过C点时对管外壁压力大小为
| ||
| D、要使球能通过C点落到垫子上,球离A点的最大高度是5R |
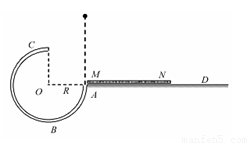




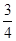 圆弧形光滑圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A 点与水平地面AD相接,地面与圆心O等高,MN 是放在水平地面上长为3R、厚度不计的减振垫,左端M正好位于A点.让游客进入一个中空的透明弹性球,人和球的总质量为m,球的直径略小于圆管直径。将球(内装有参与者)从A处管口正上方某处由静止释放后,游客将经历一个“翻天滚地”的刺激过程。不考虑空气阻力,弹性球可看作质点。那么以下说法中正确的是 (
)
圆弧形光滑圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A 点与水平地面AD相接,地面与圆心O等高,MN 是放在水平地面上长为3R、厚度不计的减振垫,左端M正好位于A点.让游客进入一个中空的透明弹性球,人和球的总质量为m,球的直径略小于圆管直径。将球(内装有参与者)从A处管口正上方某处由静止释放后,游客将经历一个“翻天滚地”的刺激过程。不考虑空气阻力,弹性球可看作质点。那么以下说法中正确的是 (
)
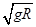

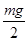

 圆弧形光滑圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A 点与水平地面AD相接,地面与圆心O等高,MN 是放在水平地面上长为3R、厚度不计的减振垫,左端M正好位于A点.让游客进入一个中空的透明弹性球,人和球的总质量为m,球的直径略小于圆管直径。将球(内装有参与者)从A处管口正上方某处由静止释放后,游客将经历一个“翻天滚地”的刺激过程。不考虑空气阻力.那么以下说法中错误的是
圆弧形光滑圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A 点与水平地面AD相接,地面与圆心O等高,MN 是放在水平地面上长为3R、厚度不计的减振垫,左端M正好位于A点.让游客进入一个中空的透明弹性球,人和球的总质量为m,球的直径略小于圆管直径。将球(内装有参与者)从A处管口正上方某处由静止释放后,游客将经历一个“翻天滚地”的刺激过程。不考虑空气阻力.那么以下说法中错误的是


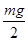 [
[
 圆弧形光滑圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A 点与水平地面AD相接,地面与圆心O等高,MN 是放在水平地面上长为3R、厚度不计的减振垫,左端M正好位于A点.让游客进入一个中空的透明弹性球,人和球的总质量为m,球的直径略小于圆管直径。将球(内装有参与者)从A处管口正上方某处由静止释放后,游客将经历一个“翻天滚地”的刺激过程。不考虑空气阻力.那么以下说法中错误的是
圆弧形光滑圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A 点与水平地面AD相接,地面与圆心O等高,MN 是放在水平地面上长为3R、厚度不计的减振垫,左端M正好位于A点.让游客进入一个中空的透明弹性球,人和球的总质量为m,球的直径略小于圆管直径。将球(内装有参与者)从A处管口正上方某处由静止释放后,游客将经历一个“翻天滚地”的刺激过程。不考虑空气阻力.那么以下说法中错误的是



