题目内容
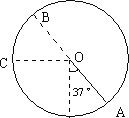
【题目】在竖直平面内有水平向右的匀强电场，场中有一根长L=2m的绝缘细线，一端固定在O点，另一端系质量为0.4kg的带电小球，静止时细线与竖直方向成37°角，如图所示。把小球缓慢拉至最低点给其一水平向右的初速度v0，为了使小球能绕O点在竖直
面内做圆周运动，求v0 应满足的条件。(cos37°=0.8，g=10m/s2)
【答案】
【解析】
根据小球在平衡位置合力为0，可以求出小球所受的电场力，根据小球恰好在竖直面内做圆周运动这一临界条件，知在平衡位置的对称点合外力提供圆周运动的向心力从而求出小球速度的最小值，根据动能定律求出v0 应满足的条件。
解：对小球进行受力分析如图所示
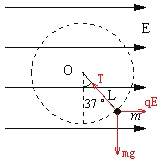
可得：
由于重力和电场力都是恒力，所以它们的合力也是恒力
在圆上各点中，小球在平衡位置A点时的势能（重力势能和电势能之和）最小，在平衡位置的对称点B点，小球的势能最大，由于小球总能量不变，所以在B点的动能EkB最小，对应速度vB最小，在B点，小球受到的重力和电场力，其合力作为小球做圆周运动的向心力，而绳的拉力恰为零，有：
解得
从最低点到B点，根据动能定律则有
联立解得 
即v0 应满足的条件
练习册系列答案
相关题目
