题目内容
【题目】如图所示，带电粒子由静止开始经电压为U1的电场加速后，射入水平放置，电势差为U2的两导体板间的匀强电场中，带电粒子沿平行于两板水平方向从两板正中间射入，穿过两板后又垂直于磁场方向射入边界线竖直的匀强磁场中，设粒子射入磁场的位置为M、射出磁场的位置为N，MN两点间的距离为d，（不计重力，不考虑边缘效应）（ ）
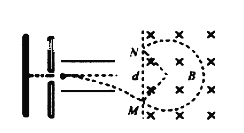
A.比荷不同的粒子射入磁场的位置M不同
B.MN两点间的距离
C.粒子在磁场中运动轨迹与U1和粒子的比荷有关，与U2无关
D.粒子在电场中运动的时间与粒子的比荷及加速电压U1和偏转电压U2有关
【答案】BC
【解析】
根据动能定理求解粒子进入偏转电场的速度大小，再根据类平抛运动求解偏转位移分析运动情况；进入磁场后，带电粒子在磁场中做匀速圆周运动，已知偏向角则由几何关系可确定圆弧所对应的圆心角，则可求得圆的半径，由洛仑兹力充当向心力可求得
表达式，再进行分析。
A．粒子在加速电场中：
解得：
设偏转电场中的极板长度为
，平行板电容器间距为
，粒子在偏转电场中的运动时的偏转位移为
，则：
由此可见粒子射出电场的偏转位移与比荷无关，比荷不同的粒子射入磁场的位置
相同，故A错误；
B．带电粒子在电场中做类平抛运动，可将射出电场的粒子速度
分解成初速度方向与加速度方向，设出射速度与水平夹角为
，则有：
而在磁场中做匀速圆周运动，设运动轨迹对应的半径为
，由几何关系可得，半径与直线
夹角正好等于，根据几何关系：
解得：
带电粒子在匀强磁场中运动的半径：
解得：
，故B正确；
C．根据上述计算结果：
可知粒子在磁场中运动轨迹与U1和粒子的比荷有关，与U2无关，故C正确；
D．粒子在加速电场中运动的时间：
为加速电场的场强，电场力提供加速度：
粒子在偏转电场中的运动的时间：
所以粒子在电场中运动的时间与粒子的比荷及加速电压
有关，和偏转电压U2无关，故D错误。
