题目内容
20．
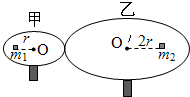如图所示，甲、乙圆盘的半径之比为1：2，两水平圆盘紧靠在一起，乙靠摩擦随甲不打滑转动．两圆盘上分别放置质量为m1和m2的小物体，m1=2m2，两小物体与圆盘间的动摩擦因数相同．m1距甲盘圆心r，m2距乙盘圆心2r，此时它们正随盘做匀速圆周运动．下列判断正确的是（ ）| A． | m1和m2的线速度之比为1：4 | B． | m1和m2的向心加速度之比为2：1 | ||
| C． | 随转速慢慢增加，m1先开始滑动 | D． | 随转速慢慢增加，m2先开始滑动 |
分析 抓住两圆盘边缘的线速度大小相等，结合圆盘的半径关系得出两圆盘的角速度之比，从而根据向心加速度公式求出向心加速度之比．抓住最大静摩擦提供向心力求出发生滑动时的临界角速度，结合甲乙的角速度进行分析判断．
解答 解：A、甲、乙两轮子边缘上的各点线速度大小相等，有：ω1•R=ω2•2R，则得ω1：ω2=2：1，所以物块相对盘开始滑动前，m1与m2的角速度之比为2：1．
根据公式：v=ωr，所以：$\frac{{v}_{1}}{{v}_{2}}=\frac{{ω}_{1}r}{{ω}_{2}•2r}=\frac{1}{1}$．故A错误．
B、根据a=ω2r得：m1与m2的向心加速度之比为 a1：a2=（ω12•r）：（ω22•2r）=2：1，故B正确．
C、D、根据μmg=mrω2=ma知，m1先达到临界角速度，可知当转速增加时，m1先开始滑动．故C正确，D错误．
故选：BC．
点评 解决本题的关键是要知道靠摩擦传动轮子边缘上的各点线速度大小相等，掌握向心加速度和角速度的关系公式和离心运动的条件．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
15．
如图所示，在a点放有带电量为Qa的电荷，在b点放有带电量为Qb的电荷，Qa、Qb为异种电荷．在它们的连线上有M、N两点，且aM=bN，比较M、N两点的场强大小和电势的高低时，发现场强EM＞EN，电势φM＜φN．则下列判断正确的是（ ）
如图所示，在a点放有带电量为Qa的电荷，在b点放有带电量为Qb的电荷，Qa、Qb为异种电荷．在它们的连线上有M、N两点，且aM=bN，比较M、N两点的场强大小和电势的高低时，发现场强EM＞EN，电势φM＜φN．则下列判断正确的是（ ）| A． | Qa为正电荷、Qb为负电荷，且|Qa|＞|Qb| | B． | Qa为正电荷、Qb为负电荷，且|Qa|＜|Qb| | ||
| C． | Qa为负电荷、Qb为正电荷，且|Qa|＞|Qb| | D． | Qa为负电荷、Qb为正电荷，且|Qa|＜|Qb| |
5．下列四个图象中，不能表示自由落体运动规律或受力特点的是（ ）
| A． |  | B． |  | C． |  | D． |  |
12．某质点做匀加速直线运动，零时刻的速度大小为3m/s，经过1s 后速度大小为4m/s，该质点的加速度大小是（ ）
| A． | 1m/s2 | B． | 7m/s2 | C． | 3m/s2 | D． | 4m/s2 |
9．
如图所示，甲、乙两个电路都由一个灵敏电流计G和一个变阻器R组成，它们中一个是测电压的电压表，另一个是测电流的电流表，那么以下结论中正确的是（ ）
如图所示，甲、乙两个电路都由一个灵敏电流计G和一个变阻器R组成，它们中一个是测电压的电压表，另一个是测电流的电流表，那么以下结论中正确的是（ ）| A． | 甲表是电流表，R增大时量程增大 | B． | 甲表是电流表，R增大时量程不变 | ||
| C． | 乙表是电压表，R增大时量程减小 | D． | 乙表是电压表，R增大时量程增大 |
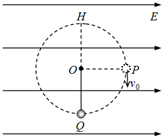如图所示，在水平向右的匀强电场中，有一根长度为L=0.4m的绝缘轻细绳，将质量为m=0.2kg、电荷量q=1.0×10-4C的带正电小球（可看成质点）悬挂在Q点，绳的悬点为O（绳可绕O点自由转动），匀强电场的场强大小E=1.5×104N/C．现将小球拉到右侧与O等高的P点（细绳伸直），以v0=2m/s的初速度竖直向下抛出，当小球下摆至最低点Q时，匀强电场方向立即变为竖直向上（场强大小不变），当小球运动到圆周的最高点H时电场立即消失．求：