题目内容
13. 某兴趣小组设计了如图所示的玩具轨道,其中“2008”四个等高数字用内壁光滑的薄壁细管弯成,固定在竖直平面内(所有数字均由圆或半圆组成,圆半径比细管的内径大得多),底端与水平地面相切.弹射装置将一个小物体(可视为质点)以v0=5m/s的水平初速度由a点弹出,从b点进入轨道,依次经过“8002”后从p点水平抛出.小物体与地面ab段间的动摩擦因数μ=0.3,已知ab段长L=1.5m,数字“0”的半径R=0.2m,小物体质量m=0.01 kg,g=10m/s2.小物体从p点抛出后的水平射程为0.8m,且在各数字的最低点的速度大小相等,求:
某兴趣小组设计了如图所示的玩具轨道,其中“2008”四个等高数字用内壁光滑的薄壁细管弯成,固定在竖直平面内(所有数字均由圆或半圆组成,圆半径比细管的内径大得多),底端与水平地面相切.弹射装置将一个小物体(可视为质点)以v0=5m/s的水平初速度由a点弹出,从b点进入轨道,依次经过“8002”后从p点水平抛出.小物体与地面ab段间的动摩擦因数μ=0.3,已知ab段长L=1.5m,数字“0”的半径R=0.2m,小物体质量m=0.01 kg,g=10m/s2.小物体从p点抛出后的水平射程为0.8m,且在各数字的最低点的速度大小相等,求:(1)小物体经过p点时的速度大小;
(2)小物体经过数字“0”的最低点时,管道对小物体作用的大小.
分析 (1)运用动能定理研究a点到p点,列出等式求出小球在P点的速度.
(2)运用动能定理研究a点到数字“0”的最低点,求出物体在数字“0”的最低点的速度大小,根据向心力公式求出管道对小物体作用的大小.
解答 解:(1)设小物体运动到P点时速度大小为vp,对小物体有a运动到P过程中应用动能定理得:
-μmgL-2mgR=$\frac{1}{2}$mvp2-$\frac{1}{2}$mva2
代入数据解得:${v}_{P}=2\sqrt{2}m/s$.
(2)设小物体运动到数字“0”的最高低时速度大小为v,对小物体由a运动到数字“0”的最低点,过程中应用动能定理得:-μmgL=$\frac{1}{2}$mv2-$\frac{1}{2}$mva2
代入数据解得:v=4m/s
在最低点,根据向心力公式得:
T-mg=m$\frac{{v}^{2}}{R}$
解得:T=0.01×$\frac{16}{0.2}+0.01×10$=0.9N
答:(1)小物体经过p点时的速度大小为$2\sqrt{2}m/s$;
(2)小物体经过数字“0”的最低点时,管道对小物体作用的大小为0.9N.
点评 本题主要考查了动能定理及向心力公式的直接应用,选取合适的研究过程,运用动能定理解题,动能定理的优点在于适用任何运动包括曲线运动.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
3.如图甲所示,理想变压器原、副线圈的匝数之比为10:1,b是原线圈的中心抽头,图中电表均为理想的交流电表,定值电阻R=10Ω,其余电阻均不计.从某时刻开始在原线圈c、d两端加上如图乙所示的交变电压.则下列说法中正确的有( )
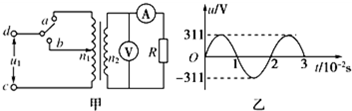

| A. | 当单刀双掷开关与a连接时,电压表的示数为22V | |
| B. | 当单刀双掷开关与a连接且在t=0.01s时,电流表示数为零 | |
| C. | 当单刀双掷开关由a拨向b时,原线圈的输入功率变大 | |
| D. | 当单刀双掷开关由a拨向b时,副线圈输出电压的频率仍为50Hz |
4.如图所示是一交变电流的i-t图象,则该交变电流的有效值为 ( )


| A. | 3A | B. | 6A | C. | 2$\sqrt{5}$A | D. | 3$\sqrt{2}$A |
1.关于环绕地球运动的卫星,下列说法正确的是( )
| A. | 由开普勒定律可知,周期越长的卫星,距地球越近 | |
| B. | 在赤道上空运行的两颗地球同步卫星,它们的轨道半径有可能不同 | |
| C. | 沿椭圆轨道运行的一颗卫星,在轨道不同位置可能具有相同的速率 | |
| D. | 沿不同轨道经过贵港上空的两颗卫星,它们的轨道平面一定会重合 |
8. 如图所示,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l,木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g,若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
如图所示,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l,木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g,若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
 如图所示,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l,木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g,若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
如图所示,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l,木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g,若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )| A. | 木块b比木块a先开始滑动 | |
| B. | 相对圆盘运动前,a、b所受的摩擦力始终相等 | |
| C. | ω=$\sqrt{\frac{2kg}{3l}}$是b开始滑动的临界角速度 | |
| D. | 当ω=$\sqrt{\frac{kg}{2l}}$时,a所受摩擦力的大小为$\frac{1}{2}$kmg |
18. 质量为2kg的物体在x-y平面做曲线运动,在x方向的速度图象和y方向的位移图象.如图所示.下列说法正确的是( )
质量为2kg的物体在x-y平面做曲线运动,在x方向的速度图象和y方向的位移图象.如图所示.下列说法正确的是( )
 质量为2kg的物体在x-y平面做曲线运动,在x方向的速度图象和y方向的位移图象.如图所示.下列说法正确的是( )
质量为2kg的物体在x-y平面做曲线运动,在x方向的速度图象和y方向的位移图象.如图所示.下列说法正确的是( )| A. | 质点所受的合外力为6N | |
| B. | 质点的初速度为5m/s | |
| C. | 2s末速度大小为6m/s | |
| D. | 质点初速度的方向与合外力方向垂直 |
5.如图所示,某物体沿$\frac{1}{4}$光滑圆弧轨道由最高点滑到最低点过程中,则( )
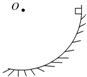

| A. | 物体的速度逐渐增大 | B. | 物体运动过程中机械能守恒 | ||
| C. | 物体所受的合外力大小保持不变 | D. | 物体所受的合外力就是向心力 |
3.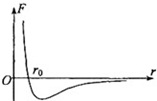 两分子间的斥力和引力的合力F与分子间距离r的关系如图中曲线所示,曲线与r轴交点的横坐标为r0.相距很远的两分子在分子力作用下,由静止开始相互接近.若两分子相距无穷远时分子势能为零,下列说法中不正确的是( )
两分子间的斥力和引力的合力F与分子间距离r的关系如图中曲线所示,曲线与r轴交点的横坐标为r0.相距很远的两分子在分子力作用下,由静止开始相互接近.若两分子相距无穷远时分子势能为零,下列说法中不正确的是( )
 两分子间的斥力和引力的合力F与分子间距离r的关系如图中曲线所示,曲线与r轴交点的横坐标为r0.相距很远的两分子在分子力作用下,由静止开始相互接近.若两分子相距无穷远时分子势能为零,下列说法中不正确的是( )
两分子间的斥力和引力的合力F与分子间距离r的关系如图中曲线所示,曲线与r轴交点的横坐标为r0.相距很远的两分子在分子力作用下,由静止开始相互接近.若两分子相距无穷远时分子势能为零,下列说法中不正确的是( )| A. | 在r>r0阶段,F做正功,分子动能增加,分子势能减小 | |
| B. | 在r<r0阶段,F做负功,分子动能减小,分子势能增大 | |
| C. | 在r=r0时,分子势能最小,分子动能最大 | |
| D. | 在r=r0时,分子势能为零 |
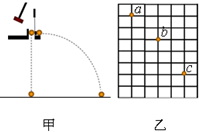 在“探究平抛运动的规律”的实验中
在“探究平抛运动的规律”的实验中