��Ŀ����
3��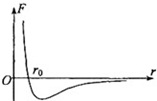 �����Ӽ�ij����������ĺ���F����Ӽ����r�Ĺ�ϵ��ͼ��������ʾ��������r�ύ��ĺ�����Ϊr0������Զ���������ڷ����������£��ɾ�ֹ��ʼ��ӽ������������������Զʱ��������Ϊ�㣬����˵���в���ȷ���ǣ�������
�����Ӽ�ij����������ĺ���F����Ӽ����r�Ĺ�ϵ��ͼ��������ʾ��������r�ύ��ĺ�����Ϊr0������Զ���������ڷ����������£��ɾ�ֹ��ʼ��ӽ������������������Զʱ��������Ϊ�㣬����˵���в���ȷ���ǣ�������| A�� | ��r��r0�Σ�F�����������Ӷ������ӣ��������ܼ�С | |
| B�� | ��r��r0�Σ�F�����������Ӷ��ܼ�С�������������� | |
| C�� | ��r=r0ʱ������������С�����Ӷ������ | |
| D�� | ��r=r0ʱ����������Ϊ�� |
���� ��ʼʱ��r��r0�Σ�������Ϊ���������������ʱ���������������������ܼ�С����r��r0��ʱ��������Ϊ����������������������������������������ݷ���������������Է����������ܵı仯��
��� �⣺A����r��r0�Σ�����������Ϊ�������������������ʱ������F�����������Ӷ������ӣ��������ܼ�С����A��ȷ��
B����r��r0�Σ�����������Ϊ�������������ʱ������F�����������Ӷ��ܼ�С��������������B��ȷ��
C�����Ϸ���֪�����������ȼ�С����������r=r0ʱ������������С���������C��ȷ��
D�����������������Զʱ��������Ϊ�㣬���ڴ�����Զ��r=r0��������һֱ����������������һֱ��С��������r=r0ʱ����������С���㣬��D����
����ѡ����ȷ�ģ���ѡ��D��
���� ���Ӽ�����ܼ���������Ȼ����������Ĺ�ϵ�����ǿ�����������ѧ������ѧ�й��ܹ�ϵ���з�����

��ϰ��ϵ�д�
 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д�
�����Ŀ
11����ī֭��ˮϡ�ͺ�ȡ��һ�Σ����������¹۲죬��ͼ��ʾ������˵������ȷ���ǣ�������


| A�� | �������¼��ܿ���ˮ����Ҳ�ܿ���������С̿������ˮ���Ӳ�ͣ��ײ��̿�� | |
| B�� | С̿���ڲ�ͣ���������˶����������˵�IJ����˶� | |
| C�� | ԽС��̿�����˶�Խ���� | |
| D�� | �������¿���������һƬ��Һ�壬ʵ���Ͼ�����������ྲֹ������ˮ������ɵ� |
18���ڸ��ٹ�·�Ĺ��䴦��·���������ڵͣ����������ҹ���ʱ��˾������·����Ҳ��Ҫ��һЩ��·����ˮƽ���ļн�Ϊ�ȣ������·���ǰ뾶ΪR��Բ����Ҫʹ����Ϊvʱ������·��֮��ĺ�����ֱ��ǰ������Ħ���������㣬��Ӧ���ڣ�������
| A�� | arcsin$\frac{{v}^{2}}{Rg}$ | B�� | arctan$\frac{{v}^{2}}{Rg}$ | C�� | $\frac{1}{2}$arcsin$\frac{2{v}^{2}}{Rg}$ | D�� | arcctg$\frac{{v}^{2}}{Rg}$ |
8���������������Ƶ���������Բ���˶�������֮��ΪTA��TB=1��8�������뾶֮�Ⱥ��˶��ٶ�֮�ȷֱ�Ϊ��������
| A�� | RA��RB=4��1��VA��VB=1��2 | B�� | RA��RB=1��4��VA��VB=1��2 | ||
| C�� | RA��RB=4��1��VA��VB=2��1 | D�� | RA��RB=1��4��VA��VB=2��1 |
15������Ϊm��������v�ij��ٶ���ֱ�����׳�����ʱ��t���ﵽ��ߵ㣬�ٶȱ�Ϊ0������ֱ����Ϊ����������������У�����Ķ����仯���������ij����ֱ��ǣ�������
| A�� | -mv��-mgt | B�� | mv��mgt | C�� | mv��-mgt | D�� | -mv��mgt |
12��һ����Ϊm���Ӿ������h�ߴ��Գ���ˮƽ�׳��������ƿ����������������˶�����صĹ����У������仯�Ĵ�СΪ��������
| A�� | m��$\sqrt{{{v}_{0}}^{2}+2gh}$-v0�� | B�� | m$\sqrt{2gh}$ | C�� | m$\sqrt{{{v}_{0}}^{2}+2gh}$ | D�� | m��$\sqrt{2gh}$-v0�� |
 ij��ȤС���������ͼ��ʾ����߹�������С�2008���ĸ��ȸ��������ڱڹ⻬�ı���ϸ����ɣ��̶�����ֱƽ���ڣ��������־���Բ���Բ��ɣ�Բ�뾶��ϸ�ܵ��ھ���öࣩ������ˮƽ�������У�����װ�ý�һ��С���壨����Ϊ�ʵ㣩��v0=5m/s��ˮƽ���ٶ���a�㵯������b������������ξ�����8002�����p��ˮƽ�׳���С���������ab�μ�Ķ�Ħ��������=0.3����֪ab�γ�L=1.5m�����֡�0���İ뾶R=0.2m��С��������m=0.01 kg��g=10m/s2��С�����p���׳����ˮƽ���Ϊ0.8m�����ڸ����ֵ���͵���ٶȴ�С��ȣ���
ij��ȤС���������ͼ��ʾ����߹�������С�2008���ĸ��ȸ��������ڱڹ⻬�ı���ϸ����ɣ��̶�����ֱƽ���ڣ��������־���Բ���Բ��ɣ�Բ�뾶��ϸ�ܵ��ھ���öࣩ������ˮƽ�������У�����װ�ý�һ��С���壨����Ϊ�ʵ㣩��v0=5m/s��ˮƽ���ٶ���a�㵯������b������������ξ�����8002�����p��ˮƽ�׳���С���������ab�μ�Ķ�Ħ��������=0.3����֪ab�γ�L=1.5m�����֡�0���İ뾶R=0.2m��С��������m=0.01 kg��g=10m/s2��С�����p���׳����ˮƽ���Ϊ0.8m�����ڸ����ֵ���͵���ٶȴ�С��ȣ��� ��ͼ��ʾ��QB��Ϊһ�뾶ΪR=1m�Ĺ⻬Բ�������AQ��Ϊһ����ΪL=1m�Ĵֲ�ˮƽ����������������Q�㣬Q��Բ��O�����·����������λ��ͬһ��ֱƽ���ڣ����P������Ϊm=1kg������Ϊ�ʵ㣩�����P���ٶ�v0=2m/s����A�㻬��ˮƽ�������C����ַ���A��ʱǡ�þ�ֹ����ȡg=10m/s2����
��ͼ��ʾ��QB��Ϊһ�뾶ΪR=1m�Ĺ⻬Բ�������AQ��Ϊһ����ΪL=1m�Ĵֲ�ˮƽ����������������Q�㣬Q��Բ��O�����·����������λ��ͬһ��ֱƽ���ڣ����P������Ϊm=1kg������Ϊ�ʵ㣩�����P���ٶ�v0=2m/s����A�㻬��ˮƽ�������C����ַ���A��ʱǡ�þ�ֹ����ȡg=10m/s2����