题目内容
8.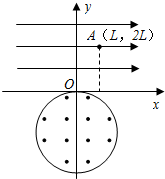 如图所示,在xOy坐标系中,x轴上方有方向沿x轴正向的匀强电场,下方有一半径为R的圆形有界匀强磁场,圆心在y轴上,且圆与x轴相切,磁场方向垂直于纸面向外,一质量为m,电量为q的带点粒子在坐标为(L,2L)的A点以初速度v0沿y轴负方向射入电场,且刚好从O点射入磁场,经磁场偏转后刚好平行于x轴从磁场中射出,求:
如图所示,在xOy坐标系中,x轴上方有方向沿x轴正向的匀强电场,下方有一半径为R的圆形有界匀强磁场,圆心在y轴上,且圆与x轴相切,磁场方向垂直于纸面向外,一质量为m,电量为q的带点粒子在坐标为(L,2L)的A点以初速度v0沿y轴负方向射入电场,且刚好从O点射入磁场,经磁场偏转后刚好平行于x轴从磁场中射出,求:(1)电场强度和磁感应强度的大小;
(2)粒子在电场和磁场中运动的总时间;
(3)若该粒子沿y轴负方向射出时的初速度大小只有$\frac{1}{2}$v0,要使该粒子也能从O点进入磁场,且经磁场偏转后刚好平行于x轴从磁场中射出,求该粒子开始射出时位置的坐标.
分析 (1)粒子在电场中做类似平抛运动,根据类平抛运动的分位移公式列式求解磁感应强度;在磁场中做匀速圆周运动,作出运动轨迹,结合几何关系得到轨道半径,然后结合推论公式r=$\frac{mv}{qB}$求解磁感应强度和运动时间;
(2)粒子在磁场中做匀速圆周运动,根据公式t=$\frac{θ}{2π}T$列式求解在磁场中的运动时间;
(3)要使粒子依然平行x轴射出,则O、磁场区域的圆心、轨迹圆心、出射点依然应该构成菱形,故粒子的轨道半径不变,故进入磁场的速度不变;对磁场中运动过程,根据平行四边形定则先求解x和y方向的分速度,然后对第一次和第二次类似平抛过程分别根据运动学公式列式后联系确定第二次释放点的坐标.
解答 解:(1)粒子在电场中做类似平抛运动,根据分位移公式,有:
$L=\frac{1}{2}\frac{qE}{m}{t}_{1}^{2}$
2L=v0t1
解得:
E=$\frac{m{v}_{0}^{2}}{2qL}$
t1=$\frac{2L}{{v}_{0}}$
速度偏转角的正切值:
tanα=2tanβ=$2×\frac{L}{2L}=1$
解得:
α=45°
由于$tanα=\frac{{v}_{y}}{{v}_{0}}$
故vy=v0
v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}=\sqrt{2}{v}_{0}$
粒子与-y方向成45°进入磁场后做匀速圆周运动,轨迹如图: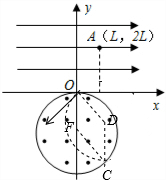
由于平行x方向射出,故∠ODC=135°,故∠OFC=135°,故可以证明,图中?ODCF为菱形,故轨道半径为:
r=R
根据推论公式r=$\frac{mv}{qB}$,解得:
B=$\frac{mv}{qr}=\frac{\sqrt{2}m{v}_{0}}{qR}$
(2)粒子在磁场中运动时间为:
t2=$\frac{135°}{360°}$•$\frac{2πr}{v}$=$\frac{3\sqrt{2}R}{{8v}_{0}}$
故粒子在电场和磁场中运动的总时间:
t=t1+t2=$\frac{2L}{{v}_{0}}$+$\frac{3\sqrt{2}R}{{8v}_{0}}$
(3)若该粒子沿y轴负方向射出时的初速度大小只有$\frac{1}{2}$v0,要使该粒子也能从O点进入磁场,且经磁场偏转后刚好平行于x轴从磁场中射出,则O、磁场区域的圆心、轨迹圆心、出射点依然应该构成菱形,故粒子的轨道半径不变,故进入磁场的速度不变,仍然为$\sqrt{2}{v}_{0}$;
由于${v}_{y}=\frac{{v}_{0}}{2}$,故${v}_{x}=\sqrt{{v}^{2}-{v}_{y}^{2}}$=$\frac{\sqrt{7}}{2}{v}_{0}$
对x方向分运动,根据速度位移公式,有:
${v}_{0}^{2}=2aL$ (第一次)
($\frac{\sqrt{7}}{2}{v}_{0}$)2=2ax′(第二次)
解得:
x′=$\frac{7}{4}L$
对y方向分运动,有:
2L=v0t1=v0$\frac{{v}_{0}}{a}$(第一次)
y′=$\frac{{v}_{0}}{2}{t}_{1}^{′}$=$\frac{{v}_{0}}{2}\frac{\frac{\sqrt{7}}{2}{v}_{0}}{a}$(第二次)
解得:
y′=$\frac{\sqrt{7}}{2}L$
故粒子第二次释放点的坐标为:($\frac{\sqrt{7}}{2}L$,$\frac{7}{4}L$)
答:(1)电场强度的大小为$\frac{m{v}_{0}^{2}}{2qL}$,磁感应强度的大小为$\frac{\sqrt{2}m{v}_{0}}{qR}$;
(2)粒子在电场和磁场中运动的总时间为$\frac{2L}{{v}_{0}}$+$\frac{3\sqrt{2}R}{{8v}_{0}}$;
(3)第二次该粒子开始射出时位置的坐标为:($\frac{\sqrt{7}}{2}L$,$\frac{7}{4}L$).
点评 本题关键是明确粒子的受力情况和运动情况,对于电场中的运动,关键是根据类似平抛运动的分运动公式列式;对于磁场中的运动,关键是明确O、磁场区域的圆心、轨迹圆心、出射点依然应该构成菱形,结合几何关系和牛顿第二定律列式分析;不难.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案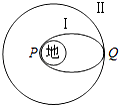 如图所示,在发射地球同步卫星的过程中,卫星首先进入椭圆轨道I,然后在Q点通过改变卫星速度,让卫星进人地球同步轨道Ⅱ,则( )
如图所示,在发射地球同步卫星的过程中,卫星首先进入椭圆轨道I,然后在Q点通过改变卫星速度,让卫星进人地球同步轨道Ⅱ,则( )| A. | 该卫星的发射速度必定大于11.2 km/s | |
| B. | 卫星在轨道上运行不受重力 | |
| C. | 在轨道I上,卫星在P点的速度大于在Q点的速度 | |
| D. | 卫星在Q点通过加速实现由轨道I进入轨道Ⅱ |
| A. | 磁感应强度 | B. | 线圈的匝数 | C. | 线圈的面积 | D. | 线圈的初始位置 |
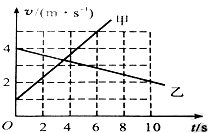
| A. | 甲的位移比乙的位移大 | B. | 甲的速度比乙的速度大 | ||
| C. | 甲的速度比乙的速度小 | D. | 甲的加速度比乙的加速度小 |
| A. | $\frac{4{\sqrt{5}v}_{0}^{2}}{g}$ | B. | $\frac{{v}_{0}^{2}}{\sqrt{5}g}$ | C. | $\frac{{\sqrt{2}v}_{0}^{2}}{2g}$ | D. | $\frac{{\sqrt{2}v}_{0}^{2}}{g}$ |
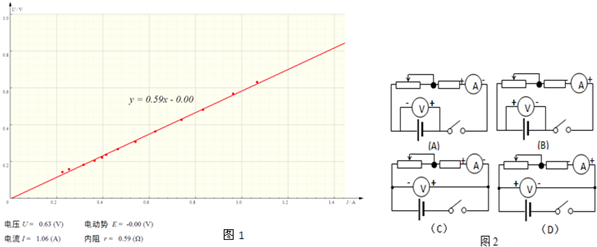
实验中,闭合开关S后,多次调节电阻箱,记下电流表的示数I和电阻箱对应的阻值R,算出$\frac{1}{I}$与$\frac{1}{R}$的值如表:
| R/Ω | 17.5 | 23.1 | 26.7 | 36.9 | 58.1 | 139.0 |
| $\frac{1}{R}$(×10-2Ω-2) | 5.71 | 4.33 | 3.75 | 2.71 | 1.72 | 0.72 |
| I/mA | 2.50 | 3.00 | 3.30 | 4.00 | 5.00 | 6.67 |
| $\frac{1}{I}$(×102A-1) | 4.00 | 3.33 | 3.03 | 2.50 | 2.00 | 1.50 |
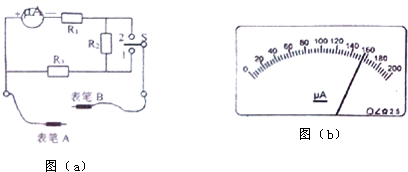
(1)根据图(a)用笔画线代替导线将图(b)中的实验器材连成实验电路.
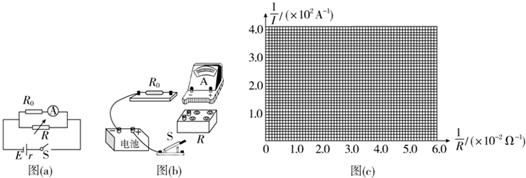
(2)$\frac{1}{I}$与$\frac{1}{R}$的关系式为$\frac{1}{I}$=$\frac{1000+r}{E}$+$\frac{1000r}{E}•\frac{1}{R}$.
(3)在图(c)的坐标纸上将所缺数据点补充完整并作图.
(4)根据图线求得电源电动势E=9.2V,内阻r=46Ω.(保留2为有效数字)
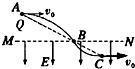 如图所示,在空间中水平面MN的下方存在竖直向下的匀强电场,质量为m的带电小球Q从水平面MN的上方A点以一定初速度v0水平抛出,从B点进入匀强电场,到达C点时速度方向恰好水平,其中A、B、C三点在同一直线上,且线段AB=2BC,由此可知( )
如图所示,在空间中水平面MN的下方存在竖直向下的匀强电场,质量为m的带电小球Q从水平面MN的上方A点以一定初速度v0水平抛出,从B点进入匀强电场,到达C点时速度方向恰好水平,其中A、B、C三点在同一直线上,且线段AB=2BC,由此可知( )| A. | 小球带正电 | |
| B. | 电场力大小为3mg | |
| C. | 小球从A到B运动的时间大于从B到C的运动时间 | |
| D. | 小球从A到B与从B到C的速度变化量相等 |