题目内容
 如图所示的力学结构,绳AO段与水平成53°角,承重不超过180N,绳BO段水平、承重不超过90N,绳CO段强度足够,在CO段的C端悬挂重物,为使力学结构不遭破坏,C端悬挂重物不能超过多少?
如图所示的力学结构,绳AO段与水平成53°角,承重不超过180N,绳BO段水平、承重不超过90N,绳CO段强度足够,在CO段的C端悬挂重物,为使力学结构不遭破坏,C端悬挂重物不能超过多少?分析:对结点O受力分析,根据AO、BO的拉力大小判断哪个绳先断,从而根据共点力平衡求出物体的最大重量.
解答:解:对O点受力如图:
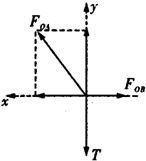
假设OB强度足够,当OA达180N时,由几何关系有:
FOB=FOA?cos53°=108N>90N,超过了OB的强度,所以BO先达强度90N.
由几何关系,有:G=T=TBO?tan53°=120N
答:为使力学结构不遭破坏,C端悬挂重物不能超过120N.

假设OB强度足够,当OA达180N时,由几何关系有:
FOB=FOA?cos53°=108N>90N,超过了OB的强度,所以BO先达强度90N.
由几何关系,有:G=T=TBO?tan53°=120N
答:为使力学结构不遭破坏,C端悬挂重物不能超过120N.
点评:解决本题的关键正确地受力分析,运用共点力平衡进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
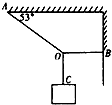 如图所示的力学结构,绳AO段与水平成53°角,承重不超过180N,绳BO段水平、承重不超过90N,绳CO段强度足够,在CO段的C端悬挂重物,为使力学结构不遭破坏,C端悬挂重物不能超过多少?
如图所示的力学结构,绳AO段与水平成53°角,承重不超过180N,绳BO段水平、承重不超过90N,绳CO段强度足够,在CO段的C端悬挂重物,为使力学结构不遭破坏,C端悬挂重物不能超过多少?





 =
=