题目内容
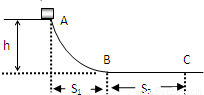
如图所示,一个质量m=50kg的物块(可视为质点)从高h=20m高台上A点由静止滑下,沿光滑的曲面滑到B点,曲面和粗糙的水平面平滑连接,滑行到C点后静止,已知A与B、B与C之间的水平距离分别为S1=30m,S2=40m,取g=10m/s2,不计空气阻力.求:(1)物块在B点的速度大小?
(2)物块在水平面BC上受到的阻力f大小.
(3)若用水平外力将物块从C由静止拉回,且在B点时撤去外力,物块恰好能上升原高度h的一半,则此外力所做的功多大?
【答案】分析:(1)选取从A-B的运动过程,运用动能定理即可求出B点速度;
(2)选取从A-C的运动过程,运用动能定理即可求出阻力f的大小;
(3)选取从C到原高度的一半,运用动能定理即可求出外力做的功.
解答:解:(1)物块从A到B由动能定理得:
mgh= mv2
mv2
解得:v=20m/s
(2)从A到C由动能定理得:
mgh-fs2=0-0
解得:f=250N
(3)从C到原高度的一半由动能定理得:
WF-fs2- mgh=0-0
mgh=0-0
解得;WF=15000J
答:(1)物块在B点的速度大小是20m/s;(2)物块在水平面BC上受到的阻力f大小是250N;(3)外力所做的功是15000J.
点评:本题考查了动能定理的直接应用.动能定理的优点在于适用任何运动包括曲线运动,一个题目可能多次选取不同的运动过程,求出不同的物理量,该题难度不大,属于基础题.
(2)选取从A-C的运动过程,运用动能定理即可求出阻力f的大小;
(3)选取从C到原高度的一半,运用动能定理即可求出外力做的功.
解答:解:(1)物块从A到B由动能定理得:
mgh=
 mv2
mv2解得:v=20m/s
(2)从A到C由动能定理得:
mgh-fs2=0-0
解得:f=250N
(3)从C到原高度的一半由动能定理得:
WF-fs2-
 mgh=0-0
mgh=0-0解得;WF=15000J
答:(1)物块在B点的速度大小是20m/s;(2)物块在水平面BC上受到的阻力f大小是250N;(3)外力所做的功是15000J.
点评:本题考查了动能定理的直接应用.动能定理的优点在于适用任何运动包括曲线运动,一个题目可能多次选取不同的运动过程,求出不同的物理量,该题难度不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,一个质量m=2kg的物体,受到与水平方向成α=370角斜向上方的拉力F=10N,在水平地面上移动的距离L=2m,地面对物体的滑动摩擦力f=4.2N(已知cos37°=0.8)求:
如图所示,一个质量m=2kg的物体,受到与水平方向成α=370角斜向上方的拉力F=10N,在水平地面上移动的距离L=2m,地面对物体的滑动摩擦力f=4.2N(已知cos37°=0.8)求: 如图所示,一个质量m=2kg的物体,受到与水平方向成37°角斜向上方的拉力F=20N,物体与地面间的动摩擦因数为μ=0.5,(已知sin37°=0.6,cos37°=0.8,g=10m/s2)
如图所示,一个质量m=2kg的物体,受到与水平方向成37°角斜向上方的拉力F=20N,物体与地面间的动摩擦因数为μ=0.5,(已知sin37°=0.6,cos37°=0.8,g=10m/s2) 如图所示,一个质量m=20kg的物块,在F=60N的水平拉力作用下,从静止开始沿水平地面向右做匀加速直线运动.物块与地面间的动摩擦因数?=0.10.取重力加速度g=10m/s2.
如图所示,一个质量m=20kg的物块,在F=60N的水平拉力作用下,从静止开始沿水平地面向右做匀加速直线运动.物块与地面间的动摩擦因数?=0.10.取重力加速度g=10m/s2.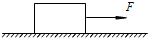 如图所示,一个质量m=2kg的物体放在光滑水平地面上.对物体施加一个F=6N的水平拉力,使物体由静止开始做匀加速直线运动.求:
如图所示,一个质量m=2kg的物体放在光滑水平地面上.对物体施加一个F=6N的水平拉力,使物体由静止开始做匀加速直线运动.求: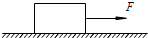 如图所示,一个质量m=10kg的物体放在光滑水平地面上.t=0时,对物体施加一水平拉力F,使物体由静止开始做匀加速直线运动;t=2.0s时,物体的速度v=6.0m/s.求:
如图所示,一个质量m=10kg的物体放在光滑水平地面上.t=0时,对物体施加一水平拉力F,使物体由静止开始做匀加速直线运动;t=2.0s时,物体的速度v=6.0m/s.求: