题目内容
6.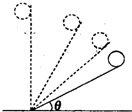 伽利略是物理学发展史上最伟大的科学家之一,如图是伽利略采用“冲淡”重力的方法,研究自由落体运动时所做的铜球沿斜面运动实验的示意图.若某同学重做此实验,让小球从长度为l、倾角为θ的斜面顶端由静止滑下,在不同的条件下进行实验,不计空气阻力及小球的转动,摩擦阻力恒定,下列叙述正确是( )
伽利略是物理学发展史上最伟大的科学家之一,如图是伽利略采用“冲淡”重力的方法,研究自由落体运动时所做的铜球沿斜面运动实验的示意图.若某同学重做此实验,让小球从长度为l、倾角为θ的斜面顶端由静止滑下,在不同的条件下进行实验,不计空气阻力及小球的转动,摩擦阻力恒定,下列叙述正确是( )| A. | l一定时,θ角越大,小球运动的加速度越小 | |
| B. | l一定时,θ角越大,小球运动时的惯性越大 | |
| C. | l一定时,θ角越大,小球从顶端运动到底端时的速度越大 | |
| D. | θ角一定时,小球从顶端运动到底端所需时间与l成正比 |
分析 对小球进行受力分析,根据牛顿第二定律求出小球运动的加速度,利用运动公式求出下滑的时间,再得到速度,即可分析.
解答 解:A、由牛顿第二定律可知 mgsinθ-μmgcosθ=ma,a=gsinθ-μgcosθ,则l一定时,θ角越大,小球运动的加速度越大,故A错误;
B、惯性只与物体的质量有关,匀运动状态无关,故B错误;
C、小球从顶端运动到底端时的速度 v=$\sqrt{2al}$=$\sqrt{2gl(sinθ-μcosθ)}$,可知l一定时,θ角越大,v越大,故C正确.
D、θ角一定时,由l=$\frac{1}{2}a{t}^{2}$,得下滑时间为 t=$\sqrt{\frac{2l}{g(sinθ-μcosθ)}}$,t与l的平方根成正比.故D错误;
故选:C.
点评 本题主要考查了牛顿第二定律与运动学公式的直接应用,注意找出个物理量与θ获L之间的关系即可.

练习册系列答案
相关题目
16.关于功和能,下列说法正确的是( )
| A. | 虽然功有正负,但功是标量 | |
| B. | 质量大的物体,动能一定大 | |
| C. | 做曲线运动的物体的动能一定变化 | |
| D. | 物体发生1m位移的过程中,作用在物体上大小为1N的力对物体做的功一定为1J |
17.在“探究加速度与力、质量的关系”的实验中,采用下图所示的装置.

(1)本实验应用的实验方法是控制变量法.下列说法中正确的是CD.
A.在探究加速度与质量的关系时,应该改变拉力的大小
B.在探究加速度与外力的关系时,应该改变小车的质量
C.在探究加速度a与质量m的关系时,为了直观判断二者间的关系,应作出a-$\frac{1}{m}$图象
D.当小车的质量远大于砝码盘和砝码的总质量时,才能近似认为细线对小车的拉力大小等于砝码盘和砝码的总重力大小
(2)某同学测得小车的加速度a和拉力F的数据如下表所示:(小车质量保持不变)
①根据表中的数据在坐标图上作出a-F图象.
②图线不过原点的原因可能是没有平衡摩擦力或摩擦力平衡不够.

(1)本实验应用的实验方法是控制变量法.下列说法中正确的是CD.
A.在探究加速度与质量的关系时,应该改变拉力的大小
B.在探究加速度与外力的关系时,应该改变小车的质量
C.在探究加速度a与质量m的关系时,为了直观判断二者间的关系,应作出a-$\frac{1}{m}$图象
| F/N | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| a/m•s-2 | 0.10 | 0.20 | 0.28 | 0.40 | 0.52 |
(2)某同学测得小车的加速度a和拉力F的数据如下表所示:(小车质量保持不变)
①根据表中的数据在坐标图上作出a-F图象.
②图线不过原点的原因可能是没有平衡摩擦力或摩擦力平衡不够.
15.用力Ff单独作用于某一物体上可产生加速度为3m/s2,力F2单独作用于这一物体产生加速度为1m/s2,若F1、F2同时作用于该物体,可能产生的加速度为( )
| A. | 1m/s2 | B. | 4m/s2 | C. | 5m/s2 | D. | 6m/s2 |
16.做平抛运动的物体,每秒的速度增量总是( )
| A. | 大小相等,方向竖直向下 | B. | 大小不等,方向竖直向下 | ||
| C. | 大小相等,方向不同 | D. | 大小不等,方向不同 |


 足球比赛中,经常使用“边路突破,下底传中”的战术,即攻方队员带球沿边线前进,到底线附近进行传中.某足球场长90m、宽60m.攻方前锋在中线处将足球沿边线向前踢出,足球的运动可视为在地面上做初速度为12m/s的匀减速直线运动,加速度大小为2m/s2.试求:
足球比赛中,经常使用“边路突破,下底传中”的战术,即攻方队员带球沿边线前进,到底线附近进行传中.某足球场长90m、宽60m.攻方前锋在中线处将足球沿边线向前踢出,足球的运动可视为在地面上做初速度为12m/s的匀减速直线运动,加速度大小为2m/s2.试求: