题目内容
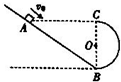
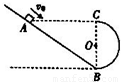
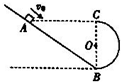所示，在竖直平面内倾斜轨道与半径为R的半圆轨道平滑连接，点A与半圆轨道的最高点C等高，B为轨道最低点，现让小滑块（可视为质点）从A点开始以初速度v0沿斜面向下运动，不计一切摩擦，重力加速度为g，关于滑块运动情况的分析，正确的是（ ）分析：物体进入右侧半圆轨道后做圆周运动，由圆周运动的临界条件可知物体能到达C点的临界值；再由机械能守恒定律可得出其在A点的速度．
解答：解：要使物体能通过最高点，则由mg=m
可得：v=
；即若速度小于
物体无法达到最高点； 若大于等于
，则可以通过最高点做平抛运动；由机械能守恒定律可知，A点的速度应大于等于
，小滑块能达到C点，且离开后做平抛运动，故C错误，D正确；
若v0=0，小滑块不能通过C点，在中间某一位置即做斜上抛运动离开轨道，故A正确，B错误；
故选AD．
| v2 |
| R |
| gR |
| gR |
| gR |
| gR |
若v0=0，小滑块不能通过C点，在中间某一位置即做斜上抛运动离开轨道，故A正确，B错误；
故选AD．
点评：机械能守恒定律与圆周运动的结合题目较为常见，在解题时一定要把握好竖直平面内圆周运动的临界值的分析．
练习册系列答案
名校课堂系列答案
相关题目
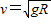，小滑块能到达C点，且离开C点后做自由落体运动
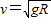，小滑块能到达C点，且离开C点后做平抛运动