题目内容
 (2011?长春二模)如果把水星和金星绕太阳的运动视为匀速圆周运动,从水星与金星在一条直线上开始计时,若天文学家测得在相同时间内水星转过的角度为θ1;金星转过的角度为θ2(θ1、θ2均为锐角),则由此条件可求得( )
(2011?长春二模)如果把水星和金星绕太阳的运动视为匀速圆周运动,从水星与金星在一条直线上开始计时,若天文学家测得在相同时间内水星转过的角度为θ1;金星转过的角度为θ2(θ1、θ2均为锐角),则由此条件可求得( )分析:相同时间内水星转过的角度为θ1;金星转过的角度为θ2,可知道它们的角速度之比,绕同一中心天体做圆周运动,根据万有引力提供向心力,可求出轨道半径比,以及向心加速度比.
解答:解:A、相同时间内水星转过的角度为θ1;金星转过的角度为θ2,可知它们的角速度之比为θ1:θ2.周期T=
,则周期比为θ2:θ1.故A正确.
B、水星和金星是环绕天体,无法求出质量,也无法知道它们的半径,所以求不出密度比.故B错误.
C、根据万有引力提供向心力:G
=mrω2,r=
,知道了角速度比,就可求出轨道半径之比.故C正确.
D、根据a=rω2,轨道半径之比、角速度之比都知道,很容易求出向心加速度之比.故D正确.
故选ACD.
| 2π |
| ω |
B、水星和金星是环绕天体,无法求出质量,也无法知道它们的半径,所以求不出密度比.故B错误.
C、根据万有引力提供向心力:G
| Mm |
| r2 |
| 3 |
| ||
D、根据a=rω2,轨道半径之比、角速度之比都知道,很容易求出向心加速度之比.故D正确.
故选ACD.
点评:解决本题的关键掌握万有引力提供向心力:G
=mrω2.以及知道要求某一天体的质量,要把该天体放在中心天体位置,放在环绕天体位置,被约去,求不出来.
| Mm |
| r2 |

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
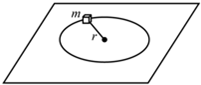 (2011?长春二模)一质量为m的质点,系在轻绳的一端,绳的另一端固定在水平面上,水平面粗糙.此质点在该水平面上做半径为r的圆周运动,设质点的最初速率是v0,当它运动一周时,其速率变为
(2011?长春二模)一质量为m的质点,系在轻绳的一端,绳的另一端固定在水平面上,水平面粗糙.此质点在该水平面上做半径为r的圆周运动,设质点的最初速率是v0,当它运动一周时,其速率变为 (2011?长春二模)[物理--选修3-3]
(2011?长春二模)[物理--选修3-3] (2011?长春二模)[物理--选修3-4]
(2011?长春二模)[物理--选修3-4] (2011?长春二模)[物理--选修3-5]
(2011?长春二模)[物理--选修3-5]