题目内容
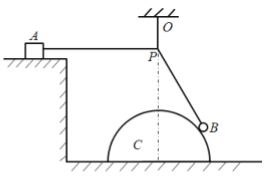
【题目】如图所示，质量为1.0kg的A物体用销钉固定在水平桌面上，左侧是半径为0.8m的光滑圆孤轨道，右侧是长为0.272m的水平轨道，圆弧轨道末端与水平轨道相切，轨道的左端比右端高0.2m，右端比桌面高0.2m。圆弧轨道的末端静置一质量为0.1kg的小物块B；将质量为0.4kg的小球C自轨道的左端最高点由静止释放，滑到圆弧轨道末端时与B块碰撞并粘在一起，此时拔掉销钉，已知物块B、小球C与水平轨道间的动摩擦因数均为0.2，A物体与桌面间的动摩擦因数为0.04，重力加速度g取10m/s2求：
(1)小球C与物块B碰撞前的速度大小；
(2)C、B碰撞粘在一起后的瞬间，对圆弧轨道的压力小；
(3)BC落到桌面上时与轨道右端的水平距离。
I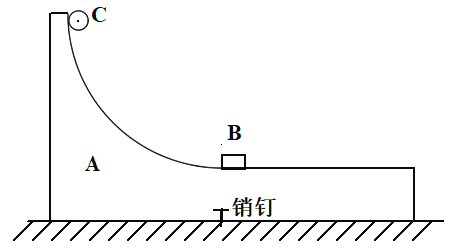
【答案】(1)
；(2)6.6N；(3)0.232m
【解析】
(1)对物体C由由静止释放到与物块B碰撞前的过程，由动能定理得
解得
(2)由C、B组成的系统碰撞前后动量守恒得
解得
由牛顿第二定律得
解得
由牛顿第三定律得对圆弧轨道的压力小
(3)对BC整体，则有
可得
对A则有
可得
物体BC与水平轨道的相对位移为
BC整体在A上滑动的时间
或
（舍）
故BC整体滑离A时的速度大小为
离
此时A的速度为
A离
由
落
可得
落
故有
落落
BC滑离A后，A的加速度大小为
而A停下来的时间
落
故在BC滑离A到落到桌面的过程中，A的位移为
故BC落到桌面上时与轨道右端的水平距离
练习册系列答案
口算小状元口算速算天天练系列答案
天天练口算系列答案
相关题目
