题目内容
(2007?盐城模拟)已知一颗人造卫星在半径为R的某行星上空绕该行星做匀速圆周运动,经过时间t,卫星运动通过的弧长为S,卫星与行星的中心连线扫过的角度是θ弧度(已知引力常量为G).求:
(1)人造卫星距该行星表面的高度h;
(2)该行星的质量M;
(3)该行星的第一宇宙速度v1.
(1)人造卫星距该行星表面的高度h;
(2)该行星的质量M;
(3)该行星的第一宇宙速度v1.
分析:(1)根据弧长等于半径乘以圆心角求解轨道半径,最后得到高度;
(2)根据万有引力定律提供向心力列式求解;
(3)行星的第一宇宙速度是近地轨道的环绕速度,根据万有引力提供向心力求解.
(2)根据万有引力定律提供向心力列式求解;
(3)行星的第一宇宙速度是近地轨道的环绕速度,根据万有引力提供向心力求解.
解答:解:(1)弧长S=rθ
高度h=r-R
故:h=
-R;
(2)线速度:v=
万有引力定律提供向心力,根据牛顿第二定律,有:
G
=m
解得:M=
;
(3)行星的第一宇宙速度是近地轨道的环绕速度,万有引力提供向心力,故
=m
解得:v1=
;
答:(1)人造卫星距该行星表面的高度h为
-R;
(2)该行星的质量M为
;
(3)该行星的第一宇宙速度为
.
高度h=r-R
故:h=
| S |
| θ |
(2)线速度:v=
| S |
| t |
万有引力定律提供向心力,根据牛顿第二定律,有:
G
| Mm |
| r2 |
| v2 |
| r |
解得:M=
| S3 |
| θGt2 |
(3)行星的第一宇宙速度是近地轨道的环绕速度,万有引力提供向心力,故
| GMm |
| R2 |
| ||
| R |
解得:v1=
|
答:(1)人造卫星距该行星表面的高度h为
| S |
| θ |
(2)该行星的质量M为
| S3 |
| θGt2 |
(3)该行星的第一宇宙速度为
|
点评:本题关键抓住万有引力提供向心力,然后根据牛顿第二定律列式求解,不难.

练习册系列答案
相关题目
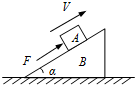 (2007?盐城模拟)如图所示,一质量为M的直角劈B放在水平面上,在劈的斜面上放一质量为m的物体A,用一沿斜面向上的力F作用于A上,使其沿斜面匀速上滑,在A上滑的过程中直角劈B相对地面始终静止,则关于地面对劈的摩擦力f及支持力N正确的是( )
(2007?盐城模拟)如图所示,一质量为M的直角劈B放在水平面上,在劈的斜面上放一质量为m的物体A,用一沿斜面向上的力F作用于A上,使其沿斜面匀速上滑,在A上滑的过程中直角劈B相对地面始终静止,则关于地面对劈的摩擦力f及支持力N正确的是( ) (2007?盐城模拟)在光滑绝缘的水平面上,用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B.A球的带电量为+2q,B球的带电量为-3q,组成一带电系统,如图所示,虚线MP为AB两球连线的垂直平分线,虚线NQ与MP平行且相距4L.最初A和B分别静止于虚线MP的两侧,距MP的距离均为L,且A球距虚线NQ的距离为3L.若视小球为质点,不计轻杆的质量,在虚线MP,NQ间加上水平向右的匀强电场E后,求:
(2007?盐城模拟)在光滑绝缘的水平面上,用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B.A球的带电量为+2q,B球的带电量为-3q,组成一带电系统,如图所示,虚线MP为AB两球连线的垂直平分线,虚线NQ与MP平行且相距4L.最初A和B分别静止于虚线MP的两侧,距MP的距离均为L,且A球距虚线NQ的距离为3L.若视小球为质点,不计轻杆的质量,在虚线MP,NQ间加上水平向右的匀强电场E后,求: