题目内容
【题目】如图甲所示,质量为![]() ,电阻为
,电阻为![]() 的金属杆ab可以无摩擦地沿水平金属轨道滑行(金属轨道电阻可以忽略不计),两轨间距为
的金属杆ab可以无摩擦地沿水平金属轨道滑行(金属轨道电阻可以忽略不计),两轨间距为![]() ,轨道一端与阻值为
,轨道一端与阻值为![]() 的电阻连接。整个轨道处于竖直向下的磁感应强度为
的电阻连接。整个轨道处于竖直向下的磁感应强度为![]() 的匀强磁场中。现在金属杆ab从
的匀强磁场中。现在金属杆ab从![]() 轴原点以初速度
轴原点以初速度![]() 向右滑行。
向右滑行。
(1)求金属杆ab刚开始滑动时,电阻![]() 两端电压U的大小;
两端电压U的大小;
(2)如果杆在滑动过程中的速度v和位移![]() 的关系满足
的关系满足![]()
①求写出杆受到的安培力的大小F随位移x变化的函数关系式,并在图乙中画出函数图象;
②要得到杆由开始滑动到静止过程中安培力所做的功,请简要说明两种方法,并证明两种方法的结果是相同的。
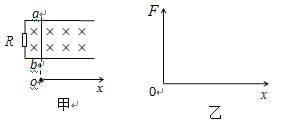
【答案】(1) ![]() (2) ①
(2) ① 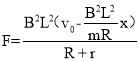
![]()
【解析】(1)金属杆ab刚开始滑动时的速度为v0,产生的感应电动势为:E0=BLv0
回路的电流![]()
电阻![]() 两端电压U的大小:U=I0R
两端电压U的大小:U=I0R
联立解得: ![]()
(2)①由法拉第电磁感应定律E= BLv其中![]()
由欧姆定律![]()
安培力F=BIL
联立解得: 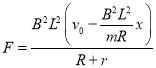
F-x图像如图:

②方法a:由图像可知,F-x为线性关系,则图像与坐标轴围成的面积等于安培力的功,由
 可知,直线与x轴交点坐标为
可知,直线与x轴交点坐标为![]() ,与F轴交点坐标为:
,与F轴交点坐标为: ![]() ,则安培力的功
,则安培力的功![]()
方法b:由能量关系可知,导体棒的动能转化为整个电路的焦耳热,其中电阻R上的焦耳热等于安培力对导体棒的功,则![]()
两种计算方法结果相同.

练习册系列答案
相关题目






