题目内容
8. 如图所示,体积为V0的导热性能良好的容器中充有一定质量的理想气体,室温为T0=300K.有一光滑导热活塞C(不占体积)将容器分成A、B两室,B室的体积是A室的两倍,气缸内气体压强为大气压的两倍,右室容器中连接有一阀门K,可与大气相通.(外界大气压等于76cmHg)求:
如图所示,体积为V0的导热性能良好的容器中充有一定质量的理想气体,室温为T0=300K.有一光滑导热活塞C(不占体积)将容器分成A、B两室,B室的体积是A室的两倍,气缸内气体压强为大气压的两倍,右室容器中连接有一阀门K,可与大气相通.(外界大气压等于76cmHg)求:①将阀门K打开后,A室的体积变成多少?
②打开阀门K后将容器内的气体从300K加热到540K,A室中气体压强为多少?
分析 ①以A中气体为研究对象,应用玻意耳定律可以求出物体的体积.
②应用盖吕萨克定律求出气体体积变为V0时气体的温度,然后应用查理定律求出气体的压强.
解答 解:①气体的初状态:PA0=2×76cmHg,VA0=$\frac{{V}_{0}}{3}$,
打开阀门,A室气体做做等温变化,PA=76cmHg,体积为VA,
由玻意耳定律:PA0VA0=PAVA,解得:VA=$\frac{2{V}_{0}}{3}$;
②温度从T0=300K升高到T,A中的气体由VA变化到V0,压强为PA,
气体做等压变化,由盖吕萨克定律得:$\frac{T}{{V}_{0}}$=$\frac{{T}_{0}}{{V}_{A}}$,解得:T=450K,
故温度从450K升高到T1=540K的过程中,
气体做等容变化,由查理定律得:$\frac{{p}_{A}}{T}$=$\frac{{p}_{A1}}{{T}_{1}}$,
解得:PA1=91.2cmHg
答:①将阀门K打开后,A室的体积变成$\frac{2{V}_{0}}{3}$;
②打开阀门K后将容器内的气体从300K加热到540K,A室中气体压强为91.2cmHg.
点评 本题考查了求气体体积、气体压强,分析清楚气体状态变化过程,求出气体的状态参量,应用气体状态方程即可解题.

练习册系列答案
相关题目
18. 图中虚线为一组间距相等的同心圆,圆心处固定一个带负电的点电荷,有一带电粒子以某一初速度射入该电场区,实线为粒子仅在电场力作用下的运动轨迹,a、b、c三点为实线和虚线的交点,则下列说法正确的是( )
图中虚线为一组间距相等的同心圆,圆心处固定一个带负电的点电荷,有一带电粒子以某一初速度射入该电场区,实线为粒子仅在电场力作用下的运动轨迹,a、b、c三点为实线和虚线的交点,则下列说法正确的是( )
 图中虚线为一组间距相等的同心圆,圆心处固定一个带负电的点电荷,有一带电粒子以某一初速度射入该电场区,实线为粒子仅在电场力作用下的运动轨迹,a、b、c三点为实线和虚线的交点,则下列说法正确的是( )
图中虚线为一组间距相等的同心圆,圆心处固定一个带负电的点电荷,有一带电粒子以某一初速度射入该电场区,实线为粒子仅在电场力作用下的运动轨迹,a、b、c三点为实线和虚线的交点,则下列说法正确的是( )| A. | a点的电势低于b点的电势 | |
| B. | 带电粒子在c点所受电场力比a点大 | |
| C. | 带电粒子在a点的电势能小于在c点的电势能 | |
| D. | 带电粒子由a点到b点的动能变化大于由b点到c点的动能变化 |
3.欧洲航天局用阿里亚娜火箭发射地球同步卫星.该卫星发射前在赤道附近(北纬5°左右)南美洲的法属圭亚那的库卢基地某个发射场上等待发射时为状态1,发射到近地轨道上做匀速圆周运动时为状态2,最后通过转移、调试,定点在地球同步轨道上时为状态3.设三个状态的半径、线速度大小、向心加速度和周期分别为r1、r2、r3,v1、v2、v3,a1、a2、a3,T1、T2、T3.则( )
| A. | v1<v3<v2,a1<a3<a2,T2<T1=T3 | B. | v1<v3<v2,a1<a3<a2,T2<T1<T3 | ||
| C. | v1>v3>v2,a1<a3<a2,T2<T1=T3 | D. | v1<v3<v2,a1<a3<a2,T2>T1>T3 |
13.质量为2m的物体A,以一定的速度沿光滑水平面运动,与一静止的物体B碰撞后粘为一体继续运动,它们共同的速度为碰撞前A的速度的$\frac{2}{3}$,则物体B的质量为( )
| A. | m | B. | 2m | C. | 3m | D. | $\frac{2}{3}$m |
20. 如图所示,楔形物体B静止在粗糙的斜面上,其质量为M,斜面倾角为θ.一质量为m的小物块A静 止在斜面上.用恒力F沿斜面向上拉小物块,小物体A仍然静止在斜面上.下列说法正确的是( )
如图所示,楔形物体B静止在粗糙的斜面上,其质量为M,斜面倾角为θ.一质量为m的小物块A静 止在斜面上.用恒力F沿斜面向上拉小物块,小物体A仍然静止在斜面上.下列说法正确的是( )
 如图所示,楔形物体B静止在粗糙的斜面上,其质量为M,斜面倾角为θ.一质量为m的小物块A静 止在斜面上.用恒力F沿斜面向上拉小物块,小物体A仍然静止在斜面上.下列说法正确的是( )
如图所示,楔形物体B静止在粗糙的斜面上,其质量为M,斜面倾角为θ.一质量为m的小物块A静 止在斜面上.用恒力F沿斜面向上拉小物块,小物体A仍然静止在斜面上.下列说法正确的是( )| A. | 没有施加恒力F时,地面对楔形物体B的支持力为Mg | |
| B. | 施加恒力F时,地面对楔形物体B的摩攘力为mgcosθ | |
| C. | 施加恒力F时,地面对楔形物体B的支持力为(M+m)g | |
| D. | 施加恒力F时,地面对楔形物体B的摩擦力为Fcosθ |
17.在物理实验中,常常有很多实验思想或方法渗透其中,下表列举了几项实验及对应的实验思想或方法,其中正确的组合是( )
| 物理实验 | 实验思想或方法 |
| ①伽利略理想斜面实验 | ⑤控制变量法 |
| ②探索加速度与力、质量的关系 | ⑥创设特定情景,揭示本质规律 |
| ③演示自由落体的真空管实验 | ⑦微元法 |
| ④探究弹簧弹性势能的表达式 | ⑧在实验事实的基础上合理外推 |
| A. | ①⑤ | B. | ②⑧ | C. | ③⑥ | D. | ④⑦ |
18.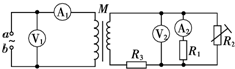 如图所示,M是一小型理想变压器,接线柱a、b接在电压u=311sin 314t(V)的正弦交变电源上.变压器右侧部分为一火警报警系统原理图,其中R2为用半导体热敏材料制成的传感器,电流表A2为值班室的显示器,显示通过R1的电流,电压表V2显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时(R2阻值变小),以下说法中正确的是( )
如图所示,M是一小型理想变压器,接线柱a、b接在电压u=311sin 314t(V)的正弦交变电源上.变压器右侧部分为一火警报警系统原理图,其中R2为用半导体热敏材料制成的传感器,电流表A2为值班室的显示器,显示通过R1的电流,电压表V2显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时(R2阻值变小),以下说法中正确的是( )
 如图所示,M是一小型理想变压器,接线柱a、b接在电压u=311sin 314t(V)的正弦交变电源上.变压器右侧部分为一火警报警系统原理图,其中R2为用半导体热敏材料制成的传感器,电流表A2为值班室的显示器,显示通过R1的电流,电压表V2显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时(R2阻值变小),以下说法中正确的是( )
如图所示,M是一小型理想变压器,接线柱a、b接在电压u=311sin 314t(V)的正弦交变电源上.变压器右侧部分为一火警报警系统原理图,其中R2为用半导体热敏材料制成的传感器,电流表A2为值班室的显示器,显示通过R1的电流,电压表V2显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时(R2阻值变小),以下说法中正确的是( )| A. | A1的示数增大,A2的示数增大 | B. | A1的示数增大,A2的示数减小 | ||
| C. | V1的示数不变,V2的示数减少 | D. | V1的示数不变,V2的示数不变 |
 如图所示,某小型水电站发电机的输出功率为10kW,输出电压为400V,向距离较远的用户供电,为了减少电能损失,使用2kV高压输电,最后用户得到220V、9.5kW的电力,求:
如图所示,某小型水电站发电机的输出功率为10kW,输出电压为400V,向距离较远的用户供电,为了减少电能损失,使用2kV高压输电,最后用户得到220V、9.5kW的电力,求: