题目内容
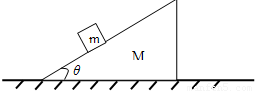
 如图所示,三角形木楔静置于粗糙水平地面上,木楔质量M=9kg、倾角θ=30°,三角形木楔的斜面上有一个质量为m=1kg的小物块.(重力加速度取g=10m/s2)
如图所示,三角形木楔静置于粗糙水平地面上,木楔质量M=9kg、倾角θ=30°,三角形木楔的斜面上有一个质量为m=1kg的小物块.(重力加速度取g=10m/s2)(1)若小物块在斜面上由静止开始下滑,当滑行距离s=1m时,其速度v=2m/s.在此过程中木楔没有动,求:
①物块下滑时所受的摩擦力大小和方向
②物块下滑时地面对木楔的摩擦力的大小和方向
(2)若小物块与斜面间的摩擦力为零,木楔与地面间的动摩擦因数为
| ||
| 15 |
分析:(1)①以小物块为研究对象.物块在斜面上由静止开始下滑,做匀加速直线运动,已知初速度、位移和末速度,根据速度位移关系式求出加速度,根据牛顿第二定律求出物块下滑时所受的摩擦力大小和方向.②以三角形木楔为研究对象,分析受力,根据共点力平衡求解地面对木楔的摩擦力的大小和方向.
(2)以小物块为研究对象,由牛顿第二定律求出加速度,再以整体为研究对象,根据牛顿第二定律求出水平恒力的大小.
(2)以小物块为研究对象,由牛顿第二定律求出加速度,再以整体为研究对象,根据牛顿第二定律求出水平恒力的大小.
解答:解:(1)①物块下滑时,则有加速度的大小为: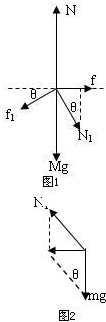
a=
=
m/s2=2m/s2
由牛顿第二定律得:
mgsinθ-f1=ma
代入解得:f1=3N,摩擦力方向沿斜面向上
②以三角形木楔为研究对象,分析受力如图1所示,物块对三角形木楔的压力N1=mgcosθ,选向右的方向为正,根据共点力平衡,在水平方向上有:
f=f1cosθ-N1sinθ=(mgsinθ-ma)cosθ-mgcosθsinθ=-macosθ
代入解得:f=-
N,负号表示地面对木楔的摩擦力的方向水平向左.
(2)以物块为研究对象,分析受力如图2所示,根据牛顿第二定律得:
mgtanθ=ma
得:a=gtanθ
代入解得:a=
m/s2
对整体在水平方向上由牛顿第二定律有:F-μ(M+m)g=(M+m)a
代入数据解得:F=40
N
答:(1)①物块下滑时所受的摩擦力大小为3N,方向沿斜面向上.
②物块下滑时地面对木楔的摩擦力的大小
N,方向水平向左.
(2)水平恒力的大小为40
N.

a=
| v2 |
| 2s |
| 22 |
| 2×1 |
由牛顿第二定律得:
mgsinθ-f1=ma
代入解得:f1=3N,摩擦力方向沿斜面向上
②以三角形木楔为研究对象,分析受力如图1所示,物块对三角形木楔的压力N1=mgcosθ,选向右的方向为正,根据共点力平衡,在水平方向上有:
f=f1cosθ-N1sinθ=(mgsinθ-ma)cosθ-mgcosθsinθ=-macosθ
代入解得:f=-
| 3 |
(2)以物块为研究对象,分析受力如图2所示,根据牛顿第二定律得:
mgtanθ=ma
得:a=gtanθ
代入解得:a=
| 10 |
| 3 |
| 3 |
对整体在水平方向上由牛顿第二定律有:F-μ(M+m)g=(M+m)a
代入数据解得:F=40
| 3 |
答:(1)①物块下滑时所受的摩擦力大小为3N,方向沿斜面向上.
②物块下滑时地面对木楔的摩擦力的大小
| 3 |
(2)水平恒力的大小为40
| 3 |
点评:本题涉及两个物体的动力学问题,要灵活选择研究对象.第1题的②问也可以对加速度不同的两个物体运用整体法处理.

练习册系列答案
相关题目
 如图所示,质量为m的三角形木楔A置于倾角为θ的固定斜面上,它与斜面间的动摩擦因数为μ,一水平力F作用在木楔A的竖直平面上.在力F的推动下,木楔A沿斜面以恒定的加速度a向上滑动,则F的大小为( )
如图所示,质量为m的三角形木楔A置于倾角为θ的固定斜面上,它与斜面间的动摩擦因数为μ,一水平力F作用在木楔A的竖直平面上.在力F的推动下,木楔A沿斜面以恒定的加速度a向上滑动,则F的大小为( )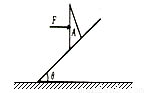
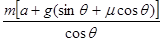 B.
B.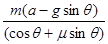
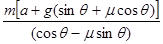 D.
D.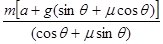
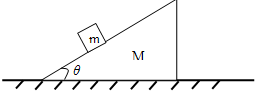 如图所示,三角形木楔静置于粗糙水平地面上,木楔质量M=9kg、倾角θ=30°,三角形木楔的斜面上有一个质量为m=1kg的小物块.(重力加速度取g=10m/s2)
如图所示,三角形木楔静置于粗糙水平地面上,木楔质量M=9kg、倾角θ=30°,三角形木楔的斜面上有一个质量为m=1kg的小物块.(重力加速度取g=10m/s2) ,有一个水平向左的恒力作用在木楔上,要使物块m相对斜面静止共同向左加速运动,求该水平恒力的大小.
,有一个水平向左的恒力作用在木楔上,要使物块m相对斜面静止共同向左加速运动,求该水平恒力的大小.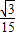 ,有一个水平向左的恒力作用在木楔上,要使物块m相对斜面静止共同向左加速运动,求该水平恒力的大小.
,有一个水平向左的恒力作用在木楔上,要使物块m相对斜面静止共同向左加速运动,求该水平恒力的大小.