Question

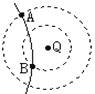
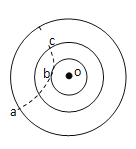
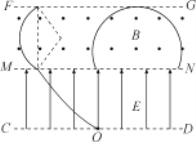
【题目】如图所示，虚线FG、MN、CD为在同一平面内的水平直线边界，在MN、CD区间内有垂直边界的匀强电场，场强的大小E＝1.5×105N/C，方向如图所示；在FG、MN区域内有垂直于纸面向外的匀强磁场，磁感应强度大小B＝0.2 T．已知电场和磁场在沿边界方向的长度均足够长，电场在垂直边界方向的宽度d1＝0.20 m．在CD边界上某点O处有一放射源，沿纸面向电场中各方向均匀地辐射出速率均为v0＝1.0×106m/s的某种带正电粒子，粒子质量m＝6.4×10－27kg，电荷量q＝3.2×10－19C，粒子可以无阻碍地通过边界MN进入磁场，不计粒子的重力及相互作用．试求：

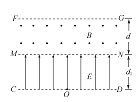
(1) 粒子在磁场中做圆周运动的半径；

(2) 要使粒子不从FG边界射出，求磁场垂直边界MN方向上的最小宽度d；

(3) 若磁场垂直边界MN方向上的宽度为0.2 m，求边界FG上有粒子射出磁场的范围长度及粒子首次在磁场中运动的最长时间．

Answer 1

【答案】(1) r＝0.2 m (2) d＝0.3 m (3)0.43m；

【解析】

只要进入磁场的粒子电场力做功是一定的，由动能定理可以求出进入磁场的速率，由洛仑兹力提供向心力就能求出粒子在磁场做匀速圆周运动的半径；先由左手定则判断出粒子做顺时针匀速圆周运动，当从边界线最左边射入磁场的轨迹与上边界相切时，此种情况下磁场区域最宽，由此画出轨迹，由几何关系就能求出磁场区域的最小宽度；由于磁场的宽度与粒子的半径相等，所以在想象中拿一个定圆在宽度一定的磁场区域移动，这样可以找到打在磁场上边缘最左端的位置--即从最左端进入磁场的粒子打在最左端，最右的位置显然是竖直向上射出的粒子恰好与上边缘相切，由几何关系求出两点的距离即为所求；至于最长时间，显然偏转角最大的--即打在最左端的粒子恰好转过半周，所以最长时间是半个周期；

(1)带电粒子从电场进入磁场，由动能定理有：

进入磁场后，洛仑兹力提供向心力：

联立两式得：，

(2)在O点水平向左或向右方向射出的粒子做类平抛运动，其偏向角与水平方向 夹角为θ，则：

所以

当从最左边射出的粒子进入磁场后是一个优弧，当该优弧与磁场上边界相切时， 由几何关系有磁场宽度为：

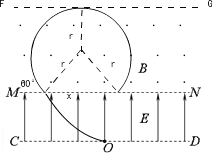
(3)水平向左射出的粒子打在A点，水平位移：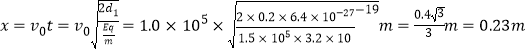

从A点与水平方向成射出的粒子做匀速圆周运动打在上边边界的P点，由对称

性，可知P点偏离O点的左边

显然从O点竖直向上射出的粒子划过四分之一圆弧打在Q点，该点是粒子打击的 最右端，由几何关系可知Q点偏离O点的右边

所以能够从FG边缘穿出的长度范围为

显然竖直向上射出的粒子恰恰在磁场中转过半周，转再回到MN，此种情况粒子在磁场中运动时间最长：