题目内容
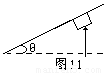
楼梯口一倾斜的天花板与水平地面成θ=37°，一装潢工人手持木杆绑着刷子粉刷天花板，工人所持木杆对刷子的作用力始终保持竖直向上，大小为F=10N，刷子的质量为m=0.5kg，刷子可视为质点，刷子与板间的动摩擦因数μ=0.5，天花板长为L=4m，取sin37°=0.6，试求：
（1）刷子沿天花板向上的加速度
（2）工人把刷子从天花板底端推到顶端所用的时间．
解：（1）以刷子为研究对象，分析受力情况，作出力图，如图．
根据牛顿第二定律得
（F-mg）sinθ-f=ma
（F-mg）cosθ-N=0
又 f=μN
联立解得 a=2m/s2
（2）刷子做匀加速运动，初速度为零，位移为L=4m，则
L=
得到 t=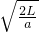
=2s
答：（1）刷子沿天花板向上的加速度为2m/s2；
（2）工人把刷子从天花板底端推到顶端所用的时间是2s．
分析：（1）以刷子为研究对象，分析受力情况：重力mg、推力F、天花板的弹力和摩擦力．根据牛顿第二定律，采用正交分解求解加速度．
（2）刷子做匀加速运动，初速度为零，位移为L=4m，结合加速度，由位移公式求出时间．
点评：本题是动力学中第一类问题：知道受力情况，确定物体的运动情况，关键是求解加速度．
根据牛顿第二定律得
（F-mg）sinθ-f=ma
（F-mg）cosθ-N=0
又 f=μN
联立解得 a=2m/s2
（2）刷子做匀加速运动，初速度为零，位移为L=4m，则
L=
得到 t=
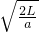=2s答：（1）刷子沿天花板向上的加速度为2m/s2；
（2）工人把刷子从天花板底端推到顶端所用的时间是2s．
分析：（1）以刷子为研究对象，分析受力情况：重力mg、推力F、天花板的弹力和摩擦力．根据牛顿第二定律，采用正交分解求解加速度．
（2）刷子做匀加速运动，初速度为零，位移为L=4m，结合加速度，由位移公式求出时间．
点评：本题是动力学中第一类问题：知道受力情况，确定物体的运动情况，关键是求解加速度．
练习册系列答案
中考解读考点精练系列答案
相关题目
楼梯口一倾斜的天花板与水平地面成θ=37°，一装潢工人手持木杆绑着刷子粉刷天花板，工人所持木杆对刷子的作用力始终保持竖直向上，大小为F=10N，刷子的质量为m=0.5kg，刷子可视为质点，刷子与板间的动摩擦因数μ=0.5，天花板长为L=4m，取sin37°=0.6，试求：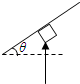
（2007?淮安模拟）楼梯口一倾斜的天花板与水平 面成θ=37°，一装潢工人手持木杆绑着刷子粉刷天花板，工人所持木杆对刷子的作用力始终保持竖直向上，大小为F=10N，刷子的质量为 m=0.5kg，刷子可视为质点．刷子与板问的动摩擦因数为0.5，扳长为L=4m，取sin37°=0.6，试求：
，一装潢工人手持木杆绑着刷子粉刷天花板，工人所持木杆对刷子的作用力始终保持竖直向上，大小为F=10N，刷子的质量为
，刷子可视为质点，刷子与板间的动摩擦因数
为0．5，天花板长为
，取
，试求：
=0.5，天花板长为L=4m，取g=10m/s2，试求：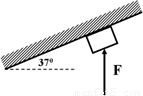 
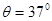，一装潢工人手持木杆绑着刷子粉刷天花板，工人所持木杆对刷子的作用力始终保持竖直向上，大小为F=10N，刷子的质量为
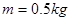，刷子可视为质点，刷子与板间的动摩擦因数
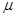为0．5，天花板长为
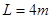，取
，试求：