题目内容
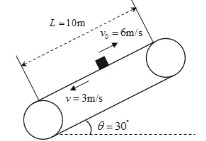
【题目】如图所示,倾角θ=30°、长度L=10m 的传送带以v=3m/s的速度稳定地逆时针传动。质量m=0.5kg、底部带有红色颜料的小滑块从距传送带底端 d=6.75m的P处,以v0=6m/s的初速度向上运动。已知滑块与传送带的动摩擦因数![]() 。试求:
。试求:
(1)滑块在传送带上运动的时间;
(2)滑块在传送带上留下的红色痕迹长度。
【答案】(1)3s;(2)6.75m.
【解析】
(1)滑块受到重力mg、支持力FN、沿斜面向下的摩擦力f作用,根据牛顿第二定律可得:
mgsinθ+f=ma
FN=mgcosθ
又
f=μFN
联立方程,代入数据得:
a=6m/s2
开始滑块向上做匀减速运动,减速到零时所有时间为
![]()
滑块向上运动的距离为
![]()
因为x<L-d,所以滑块还没有到达传动带最高点时速度已经为零,以后滑块将沿传送带向下以加速度a做匀加速运动,设经时间t2与传送带速度相等,则:
![]()
向下运动的位移为
![]()
滑块速度与传送带速度相等时,滑块所受摩擦力方向变为沿传送带向上,因为
![]()
所以滑块将继续沿传送带向下加速运动,加速度为a′,由牛顿第二定律可得
mgsinθ-μmgcosθ=ma′
代入数据解得
a′=4m/s2
从滑块与传送带速度相等开始,滑块达到底端的时间为t3,达到底部的速度为v1,达到底部时的位移为
x2=d+x-x1=9m
根据速度位移关系可得
v12-v2=2a′x2
解得
v1=9m/s
则
![]()
滑块在传送带上运动的时间为
t=t1+t2+t3=3s
(2)滑块减速上升过程中相对于传送带向上滑动的距离为
△x1=x+vt1=6m
滑块加速下滑到与传送带共速过程中相对于传送带向上滑动的距离为
△x2=vt2-x1=0.75m
从滑块与传送带速度相等开始到滑块达到底端的过程中相对于传送带向下滑动的距离为
△x3=x2-vt3=4.5m
由于红色痕迹有重叠,故滑块在传送带上留下的红色痕迹长度为
△x=△x1+△x2=6.75m