题目内容
【题目】假设在半径为R的某天体上发射一颗该天体的卫星.若它贴近该天体的表面做匀速圆周运动的周期为T 1 ,已知万有引力常量为G.
(1)则该天体的密度是多少？
(2)若这颗卫星距该天体表面的高度为h,测得在该处做圆周运动的周期为T 2 ,则该天体的密度又是多少？
(3)比较例题中的两个结果,说明开普勒第三定律 
中k与什么因素有关？
(4)若用弹簧测力计测得该星体表面一质量为m的物体的重力为F.则该星体的密度.
【答案】(1) 
； (2) 
；(3)k只与中心天体的质量有关.不同的天体k值不同 ；(4) 
【解析】(1)设卫星的质量为m,天体的质量为M,卫星贴近天体表面运动时有 
解得
根据数学知识可知星球的体积为V=
πR 3
故该星球密度为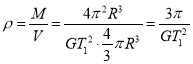
(2)卫星距天体表面距离为h时,有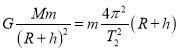 
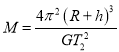
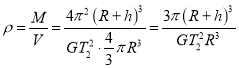
(3)由
得 
由
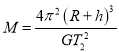得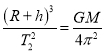 
由此可见,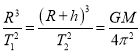 
=k，所以k只与中心天体的质量有关,与行星、卫星均无关.
(4)设该星体表面的重力加速度为g，则F=mg， 
，
忽略星体的自转,物体所受重力的大小等于万有引力的大小 
则
.
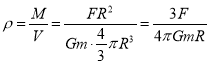练习册系列答案
相关题目
