题目内容
一列横波在x轴上传播,a、b是x轴上相距Sab=6m的两质点.t=0时,b点正好到达最高点,且b点到x轴的距离为2cm,而此时a点恰好经过平衡位置向下运动,已知这列波的频率为25Hz.
(1)求经过时间1s,a质点运动的路程;
(2)设a、b在x轴上的距离大于一个波长而小于两个波长,求该列横波的波速.
(3)若该列横波由a向b方向传播,且a、b在x轴上的距离大于一个波长而小于两个波长,a的平衡位置在x=0处,试画出a、b之间t=0.01s时刻的波形图.
(1)求经过时间1s,a质点运动的路程;
(2)设a、b在x轴上的距离大于一个波长而小于两个波长,求该列横波的波速.
(3)若该列横波由a向b方向传播,且a、b在x轴上的距离大于一个波长而小于两个波长,a的平衡位置在x=0处,试画出a、b之间t=0.01s时刻的波形图.
分析:(1)简谐运动1s内传播的路程等于振幅的四倍;
(2)b在最高点时,a在平衡位置且向上运动,故ab间距离为1.75、2.75、3.75、…倍波长,求解出波长后根据v=λf求解波速.
(2)b在最高点时,a在平衡位置且向上运动,故ab间距离为1.75、2.75、3.75、…倍波长,求解出波长后根据v=λf求解波速.
解答:解:(1)质点a一个周期运动的路程等于4倍振幅,1s内运动的路程为:S0=4×0.02m=0.08m…①
1s内的周期数是n=ft=25…②
1s内运动的路程S=nS0=2m…③
(2)波由b传向a,Sab=(1+
)λ…④
v=λf=
=
=
m/s=…⑤
波由a传向b,Sab=(1+
)
v=λf=
m/s=
=120m/s…⑦
(3)若该列横波由a向b方向传播则a、b在x轴上的距离为1
λ=6m,则λ=4.8m
a、b之间t=0.01s时刻的波形图为:
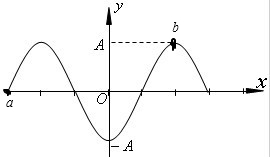
答:(1)过时间1s,a质点运动的路程为2m;
(2)设a、b在x轴上的距离大于一个波长,若波由b向a传播,波速为
m/s;若波由a向b传播波速为120m/s;
(3)如图.
1s内的周期数是n=ft=25…②
1s内运动的路程S=nS0=2m…③
(2)波由b传向a,Sab=(1+
| 3 |
| 4 |
v=λf=
| 600 |
| 4n+3 |
| 600 |
| 4+3 |
| 600 |
| 7 |
波由a传向b,Sab=(1+
| 1 |
| 4 |
v=λf=
| 600 |
| 4n+1 |
| 600 |
| 5 |
(3)若该列横波由a向b方向传播则a、b在x轴上的距离为1
| 1 |
| 4 |
a、b之间t=0.01s时刻的波形图为:

答:(1)过时间1s,a质点运动的路程为2m;
(2)设a、b在x轴上的距离大于一个波长,若波由b向a传播,波速为
| 600 |
| 7 |
(3)如图.
点评:本题难点在于根据题意得到ab间的间距与波长的关系,然后根据公式v=λf求解波速.

练习册系列答案
相关题目
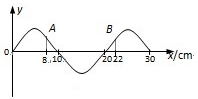 一列横波在x轴上传播,频率为5Hz,某时刻的波形如图所示,其中xA=8cm,xB=22cm.从此时刻起,欲使质点B的运动状态与质点A在图示时刻的运动状态完全相同,则至少要经过的时间可能是( )
一列横波在x轴上传播,频率为5Hz,某时刻的波形如图所示,其中xA=8cm,xB=22cm.从此时刻起,欲使质点B的运动状态与质点A在图示时刻的运动状态完全相同,则至少要经过的时间可能是( )| A、0.06s | B、0.10s | C、0.14s | D、0.26s |
 (2011?静安区二模)一列横波在x轴上传播,在某时刻波形图如图所示,已知此时质点E的运动方向向下,则( )
(2011?静安区二模)一列横波在x轴上传播,在某时刻波形图如图所示,已知此时质点E的运动方向向下,则( )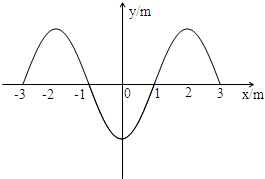 一列横波在X轴上传播,t时刻与t+0.4s时刻在X轴上-3m~3m的区间内的波形图如图所示,由图可知( )
一列横波在X轴上传播,t时刻与t+0.4s时刻在X轴上-3m~3m的区间内的波形图如图所示,由图可知( )