题目内容
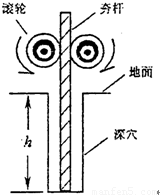
图示是建筑工地常用的一种“深穴打夯机”.工作时,电动机带动两个紧压夯杆的滚轮匀速转运将夯杆从深为h的坑中提上来,当两个滚轮彼此分开时,夯杆被释放,最后夯在自身重力作用下,落回深坑,夯实坑底.然后,两个滚轮再次压紧,夯杆再次被提上来,如此周而复始工作.已知两个滚轮边缘线速度v恒为4m/s,每个滚轮对夯杆的正压力FN为2×104N,滚轮与夯杆间的动摩擦因数μ为0.3,夯杆质量m为1×103kg,坑深h为6.4m.假定在打夯的过程中坑的深度变化不大,且夯杆底端升到坑口时,速度正好为零.取g=10m/s2.求:(1)夯杆上升过程中被滚轮释放时的速度为多大,此时夯杆底端离夯底多高;
(2)每个打夯周期中,电动机对夯杆所作的功;
(3)打夯周期.
【答案】分析:(1)求出夯杆受到的摩擦力,从而求出夯杆向上匀加速运动的加速度a,通过计算判断夯杆上升运动的过程从而确定夯杆被释放时速度和离夯底的高度;
(2)重力和电动机对夯杆做功,根据动能定理可以求出电动机做的功;
(3)根据(1)问的分析,分匀加速上升、匀速上升和匀减速上升以及自由下落四段求一个打夯周期的时间.
解答:解:(1)夯杆在上升过程中,对夯杆进行受力分析知,夯杆所受摩擦力为: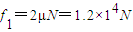 ;
;
夯杆产生加速度为: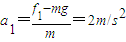
当夯杆与滚轮相对静止时: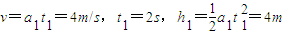
当夯杆以v=4m/s的初速度竖直上抛,上升高度为: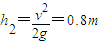
则当夯杆加速向上运动速度到达v=4m/s后,夯杆匀速上升,匀速上升高度为:h3=h-h1-h2=1.6m
因此,夯杆先匀加速上升,后匀速上升,再竖直上抛.
故夯杆上升过程中被滚轮释放时的速度为4m/s;
此时夯杆底端离夯底△h=h-h2=5.6m.
(2)夯杆在上升过程中只有电动机和重力对夯杆做功,根据动能定理有:
W+WG=0
∴W=-WG=-mg(-h)=mgh=6.4×104J
夯杆下落过程中只有重力做功电动机不做功,故一个打夯周期中电动机对夯杆做功为6.4×104J
(3)夯杆上抛运动的时间为: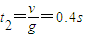 ;
;
夯杆匀速上升的时间为: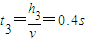 ;
;
夯杆自由落体的时间为: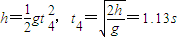
故打夯周期为:T=t1+t2+t3+t4=3.93s
答:(1)夯杆上升过程中被滚轮释放时的速度为4m/s,此时夯杆底端离夯底5.6m;
(2)每个打夯周期中,电动机对夯杆所作的功6.4×104J;
(3)打夯周期为3.93s.
点评:本题关键是分析求出夯杆的运动规律,根据牛顿第二定律和运动学公式综合求解.
(2)重力和电动机对夯杆做功,根据动能定理可以求出电动机做的功;
(3)根据(1)问的分析,分匀加速上升、匀速上升和匀减速上升以及自由下落四段求一个打夯周期的时间.
解答:解:(1)夯杆在上升过程中,对夯杆进行受力分析知,夯杆所受摩擦力为:
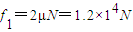 ;
;夯杆产生加速度为:
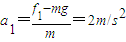
当夯杆与滚轮相对静止时:
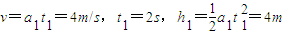
当夯杆以v=4m/s的初速度竖直上抛,上升高度为:
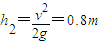
则当夯杆加速向上运动速度到达v=4m/s后,夯杆匀速上升,匀速上升高度为:h3=h-h1-h2=1.6m
因此,夯杆先匀加速上升,后匀速上升,再竖直上抛.
故夯杆上升过程中被滚轮释放时的速度为4m/s;
此时夯杆底端离夯底△h=h-h2=5.6m.
(2)夯杆在上升过程中只有电动机和重力对夯杆做功,根据动能定理有:
W+WG=0
∴W=-WG=-mg(-h)=mgh=6.4×104J
夯杆下落过程中只有重力做功电动机不做功,故一个打夯周期中电动机对夯杆做功为6.4×104J
(3)夯杆上抛运动的时间为:
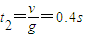 ;
; 夯杆匀速上升的时间为:
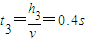 ;
; 夯杆自由落体的时间为:
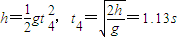
故打夯周期为:T=t1+t2+t3+t4=3.93s
答:(1)夯杆上升过程中被滚轮释放时的速度为4m/s,此时夯杆底端离夯底5.6m;
(2)每个打夯周期中,电动机对夯杆所作的功6.4×104J;
(3)打夯周期为3.93s.
点评:本题关键是分析求出夯杆的运动规律,根据牛顿第二定律和运动学公式综合求解.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
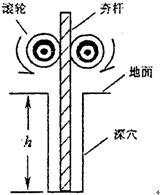 (2006?滨州二模)图示是建筑工地常用的一种“深穴打夯机”.工作时,电动机带动两个紧压夯杆的滚轮匀速转运将夯杆从深为h的坑中提上来,当两个滚轮彼此分开时,夯杆被释放,最后夯在自身重力作用下,落回深坑,夯实坑底.然后,两个滚轮再次压紧,夯杆再次被提上来,如此周而复始工作.已知两个滚轮边缘线速度v恒为4m/s,每个滚轮对夯杆的正压力FN为2×104N,滚轮与夯杆间的动摩擦因数μ为0.3,夯杆质量m为1×103kg,坑深h为6.4m.假定在打夯的过程中坑的深度变化不大,且夯杆底端升到坑口时,速度正好为零.取g=10m/s2.求:
(2006?滨州二模)图示是建筑工地常用的一种“深穴打夯机”.工作时,电动机带动两个紧压夯杆的滚轮匀速转运将夯杆从深为h的坑中提上来,当两个滚轮彼此分开时,夯杆被释放,最后夯在自身重力作用下,落回深坑,夯实坑底.然后,两个滚轮再次压紧,夯杆再次被提上来,如此周而复始工作.已知两个滚轮边缘线速度v恒为4m/s,每个滚轮对夯杆的正压力FN为2×104N,滚轮与夯杆间的动摩擦因数μ为0.3,夯杆质量m为1×103kg,坑深h为6.4m.假定在打夯的过程中坑的深度变化不大,且夯杆底端升到坑口时,速度正好为零.取g=10m/s2.求: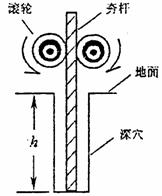 (1)夯杆上升过程中被滚轮释放时的速度为多大,此时夯杆底端离夯底多高;
(1)夯杆上升过程中被滚轮释放时的速度为多大,此时夯杆底端离夯底多高;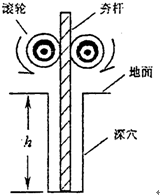 图示是建筑工地常用的一种“深穴打夯机”.工作时,电动机带动两个紧压夯杆的滚轮匀速转运将夯杆从深为h的坑中提上来,当两个滚轮彼此分开时,夯杆被释放,最后夯在自身重力作用下,落回深坑,夯实坑底.然后,两个滚轮再次压紧,夯杆再次被提上来,如此周而复始工作.已知两个滚轮边缘线速度v恒为4m/s,每个滚轮对夯杆的正压力FN为2×104N,滚轮与夯杆间的动摩擦因数μ为0.3,夯杆质量m为1×103kg,坑深h为6.4m.假定在打夯的过程中坑的深度变化不大,且夯杆底端升到坑口时,速度正好为零.取g=10m/s2.求:
图示是建筑工地常用的一种“深穴打夯机”.工作时,电动机带动两个紧压夯杆的滚轮匀速转运将夯杆从深为h的坑中提上来,当两个滚轮彼此分开时,夯杆被释放,最后夯在自身重力作用下,落回深坑,夯实坑底.然后,两个滚轮再次压紧,夯杆再次被提上来,如此周而复始工作.已知两个滚轮边缘线速度v恒为4m/s,每个滚轮对夯杆的正压力FN为2×104N,滚轮与夯杆间的动摩擦因数μ为0.3,夯杆质量m为1×103kg,坑深h为6.4m.假定在打夯的过程中坑的深度变化不大,且夯杆底端升到坑口时,速度正好为零.取g=10m/s2.求: