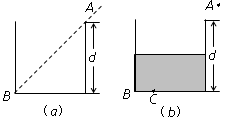Question

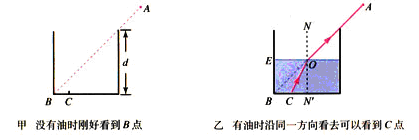
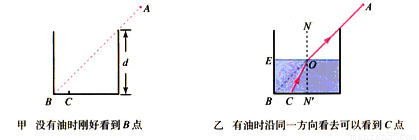
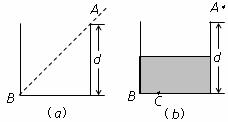
一个储油桶的底面直径与高均为d．当桶内没有油时，从某点A恰能看到桶底边缘的某点B．如图 （a）所示，当桶内油的深度等于桶高的一半时，仍沿AB方向看去，恰好看到桶底上的点C，如图（b）所示，C、B两点相距d/4．（

5

≈2.2，

2

≈1.4．） 求
（1）试在图（b）中画出光路的示意图
（2）油的折射率
（3）光在油中传播的速度．

Answer 1

分析：根据几何关系求出入射角和折射角，结合折射定律求出油的折射率，根据v=

c

n

求出光在油中的传播速度．

解答：解：（1）光路如图（c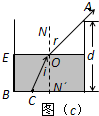）所示．
（2）由题意知，底面直径与桶高相等，所以图中角r=45°，角i
可以计算出sini=

CN′

CN′2+ON′2

=

d 4

5 d 4

=

5

5

所以油的折射率n=

sinr

sini

=

5 2

≈1.6
（3）由于n=

c

v

所以光在油中的速度v=

c

n

=

3×108

5 2

≈1.9×108m/s．
答：（1）光路图如图所示．
（2）油的折射率为1.6．
（3）光在油中传播的速度为1.9×10⁸m/s．

点评：本题考查几何光学问题，对数学几何要求能力较高，关系是确定入射角和折射角，通过折射定律进行解决．