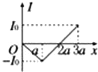Question

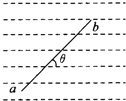
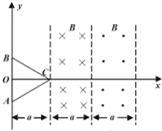
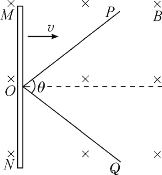
【题目】如图所示，两根完全相同的光滑金属导轨OP、OQ固定在水平桌面上，导轨间的夹角为θ=74°．导轨所在空间有垂直于桌面向下的匀强磁场，磁感应强度大小为B0=0．2 T．t=0时刻，一长为L=1m的金属杆MN在外力作用下以恒定速度v=0．2m/s从O点开始向右滑动．在滑动过程中金属杆MN与导轨接触良好，且始终垂直于两导轨夹角的平分线，金属杆的中点始终在两导轨夹角的平分线上．导轨与金属杆单位长度（1m）的电阻均为r0=0．1 Ω．sin 37°=0．6．

（1）求=2s时刻，金属杆中的感应电动势E和此时闭合回路的总长度．

（2）求=2s时刻，闭合回路中的感应电流I．

（3）若在=2s时刻撤去外力，为保持金属杆继续以v=0．2m/s做匀速运动，在金属杆脱离导轨前可采取将B从B0逐渐减小的方法，从撤去外力开始计时的时间为，则磁感应强度B应随时间怎样变化（写出B与的关系式）．

Answer 1

【答案】（1）0．024V，1．6m

（2）0．15 A．

（3）B= （0 s≤t2≤s）．

【解析】

试题（1）在t1时刻，连入回路的金属杆的长度 L=2vttan 37°=1．5v，

回路的电动势E=B0Lv=1．5 B0v2 t1=0．024V，

回路的总长度：s=1．6m

（2）回路的电阻R=0．4v=0．16Ω，

回路的电流I==0．75v=0．15 A．

（3）在t1=2 s时刻撤去外力后，因金属杆做匀速运动，故光滑金属杆不再受到安培力作用，回路的感应电流为零，任一时刻回路磁通量相等Φ1=Φ2，

三角形回路的面积S=，

t1=2 s时刻回路的磁通量Φ1=B0，

再过时间t2回路的磁通量Φ2=B，

B0= B

联立解得B= （0 s≤t2≤s）．

或写成B= （0 s≤t2≤s）．