题目内容
 如图所示,宽度为d的有界匀强磁场,磁感应强度为B,MM′和NN′是它的两条边界.现有质量为m,电荷量为q的带电粒子沿图示方向垂直磁场射入.要使粒子不能从边界NN′射出,求粒子入射速率v的最大值.
如图所示,宽度为d的有界匀强磁场,磁感应强度为B,MM′和NN′是它的两条边界.现有质量为m,电荷量为q的带电粒子沿图示方向垂直磁场射入.要使粒子不能从边界NN′射出,求粒子入射速率v的最大值.分析:带电粒子垂直射入匀强磁场时,做匀速圆周运动,速度越大,粒子的轨迹半径越大,当轨迹恰好与边界NN′相切时,粒子恰好不能从边界NN′射出,根据几何知识求出轨迹半径,由牛顿第二定律求解粒子入射速率的最大值.由于题中没有说明带电粒子的电性,要分正电和负电两种情况求解.
解答: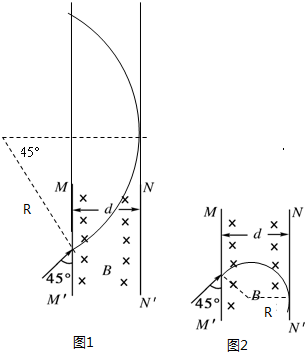 解:题目中只给出粒子“电荷量为q”,未说明是带哪种电荷.若带正电荷,轨迹是如图所示上方与NN′相切的
解:题目中只给出粒子“电荷量为q”,未说明是带哪种电荷.若带正电荷,轨迹是如图所示上方与NN′相切的
圆弧,如图1所示.
设轨道半径为R,根据几何知识得:
R-Rcos45°=d
解得:R=(2+
)d
粒子在磁场中运动时由洛伦兹力提供向心力,则牛顿第二定律得:
qvB=m
解得:v=(2+
)
.
若带负电荷,轨迹如图所示下方与NN′相切的
圆弧,如图2所示.根据几何知识得:
R+Rcos45°=d
解得:R=(2-
)d
由qvB=m
解得:v=(2-
)
.
答:粒子入射速率v的最大值是(2+
)
或(2-
)
.
 解:题目中只给出粒子“电荷量为q”,未说明是带哪种电荷.若带正电荷,轨迹是如图所示上方与NN′相切的
解:题目中只给出粒子“电荷量为q”,未说明是带哪种电荷.若带正电荷,轨迹是如图所示上方与NN′相切的| 1 |
| 4 |
设轨道半径为R,根据几何知识得:
R-Rcos45°=d
解得:R=(2+
| 2 |
粒子在磁场中运动时由洛伦兹力提供向心力,则牛顿第二定律得:
qvB=m
| v2 |
| R |
解得:v=(2+
| 2 |
| Bqd |
| m |
若带负电荷,轨迹如图所示下方与NN′相切的
| 3 |
| 4 |
R+Rcos45°=d
解得:R=(2-
| 2 |
由qvB=m
| v2 |
| R |
解得:v=(2-
| 2 |
| Bqd |
| m |
答:粒子入射速率v的最大值是(2+
| 2 |
| Bqd |
| m |
| 2 |
| Bqd |
| m |
点评:对于带电粒子在磁场中运动的轨迹问题,画出轨迹,运用几何知识求轨迹半径是经常采用的方法,要加强数学能力的培养,提高解题能力.

练习册系列答案
相关题目
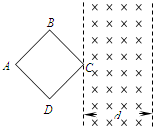 如图所示,宽度为d的有界匀强磁场,方向垂直于纸面向里.在纸面所在平面内有一对角线长也为d的正方形闭合导线ABCD,沿AC方向垂直磁场边界,匀速穿过该磁场区域.规定逆时针方向为感应电流的正方向,t=0时C点恰好进入磁场,则从C点进入磁场开始到A点离开磁场为止,闭合导线中感应电流随时间的变化图象正确的是( )
如图所示,宽度为d的有界匀强磁场,方向垂直于纸面向里.在纸面所在平面内有一对角线长也为d的正方形闭合导线ABCD,沿AC方向垂直磁场边界,匀速穿过该磁场区域.规定逆时针方向为感应电流的正方向,t=0时C点恰好进入磁场,则从C点进入磁场开始到A点离开磁场为止,闭合导线中感应电流随时间的变化图象正确的是( )
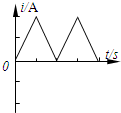


 如图所示,宽度为d的区域上下分别存在垂直纸面、方向相反、磁感应强度大小均为B的匀强磁场.现有一质量为m、电量为+q的粒子,在纸面内以速度V从此区域下边缘上的A点射入,其方向与下边缘成30°角,试求
如图所示,宽度为d的区域上下分别存在垂直纸面、方向相反、磁感应强度大小均为B的匀强磁场.现有一质量为m、电量为+q的粒子,在纸面内以速度V从此区域下边缘上的A点射入,其方向与下边缘成30°角,试求 如图所示,宽度为d的有界匀强磁场竖直向下穿过光滑的水平桌面,一质量为m的椭圆形导体框平放在桌面上,椭圆的长轴平行磁场边界,短轴小于d.现给导体框一个初速度v0(v0垂直磁场边界),已知导体框全部在磁场中的速度为v,导体框全部出磁场后的速度为v1;导体框进入磁场过程中产生的焦耳热为Q1,导体框离开磁场过程中产生的焦耳热为Q2.下列说法正确的是( )
如图所示,宽度为d的有界匀强磁场竖直向下穿过光滑的水平桌面,一质量为m的椭圆形导体框平放在桌面上,椭圆的长轴平行磁场边界,短轴小于d.现给导体框一个初速度v0(v0垂直磁场边界),已知导体框全部在磁场中的速度为v,导体框全部出磁场后的速度为v1;导体框进入磁场过程中产生的焦耳热为Q1,导体框离开磁场过程中产生的焦耳热为Q2.下列说法正确的是( )