题目内容
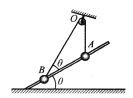
【题目】2016年新春佳节,许多餐厅生意火爆,常常人满为患,为能服务更多的顾客,服务员需要用最短的时间将菜肴送至顾客处(设菜品送到顾客处速度恰好为零)。某次服务员用单手托托盘方式(如图)给12 m远处的顾客上菜,要求全程托盘水平。托盘和手、碗之间的动摩擦因数分别为0.2、0.15,服务员上菜时的最大速度为3 m/s。假设服务员加速、减速过程中做匀变速直线运动,且可认为最大静摩擦力等于滑动摩擦力。已知重力加速度g=10 m/s2。

(1)求服务员运动的最大加速度;
(2)求服务员上菜所用的最短时间。
【答案】(1)1.5m/s2;(2)6s.
【解析】试题分析:(1)设碗的质量为m,托盘的质量为M,以最大加速度运动时,碗、托盘、手保持相对静止,碗受力如图甲所示,由牛顿第二定律得:Ff1=ma1,
碗与托盘间相对静止,则:Ff1≤Ff1max=μ1mg,
解得:a1≤μ1g=0.15×10=1.5m/s2,
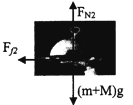
对碗和托盘整体,由牛顿第二定律得:Ff2=(M+m)a2,
手和托盘间相对静止,则:Ff2≤Ff2max=μ2(M+m)g,
解得:a2≤μ2g=0.2×10=2m/s2,
则最大加速度:amax=1.5m/s2;
(2)服务员以最大加速度达到最大速度,然后匀速运动,再以最大加速度减速运动,所需时间最短,
加速运动时间: ![]() ,
,
位移:![]() ,
,
减速运动时间:t2=t1=2s,位移:x2=x1= 3m,
匀速运动位移:x3=L-x1-x2=12m- 3m - 3m = 6m
匀速运动时间: ![]() ,
,
最短时间:t=t1+t2+t3=6s

练习册系列答案
相关题目