��Ŀ����
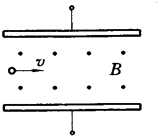
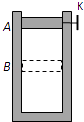
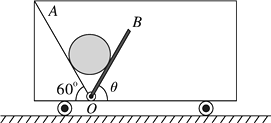
����Ŀ����ͼ��ʾ��M��N���㹻����ˮƽ��Ե��������ΪR�����㣬MN�����ֲڣ����ಿ�ֹ⻬������MNΪ�߽����ֱ�ռ��һ����ǿ�������ҵ���ǿ�糡����N����Ҳ���һ����ΪR������O������ֱ��������ת������ˣ�����¶˹̶�һ������Ϊm��С��B��B����ǡ�ýӴ�û�м�ѹ������һ�������������Ϊm�����A����M�����ٶ�v0���ҽ���糡������֪A����MN���Ħ����f= ![]() mg��A���ܵĵ糡��F=mg����A��B���Կ����ʵ㣬����������A�ĵ�������ֲ��䣬��
mg��A���ܵĵ糡��F=mg����A��B���Կ����ʵ㣬����������A�ĵ�������ֲ��䣬��
��1����v0= ![]() ����A�����˶��뿪�糡��B��һ����ײǰ�ٶȶ��
����A�����˶��뿪�糡��B��һ����ײǰ�ٶȶ��
��2����v0= ![]() ��A��B��һ����ײ��B��պ��ܵ�����ߵ㣬��AB��ײ��������ʧ���ٻ�е�ܣ�
��A��B��һ����ײ��B��պ��ܵ�����ߵ㣬��AB��ײ��������ʧ���ٻ�е�ܣ�
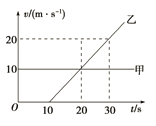
��3����B�ɵ���С��A��Bÿ����ײ�������ٶȣ���0��v0�� ![]() ��������A�ڵ糡��ͨ������·����v0�Ĺ�ϵ��
��������A�ڵ糡��ͨ������·����v0�Ĺ�ϵ��
���𰸡�
��1���⣺��A�����˶��뿪�糡ʱ���ٶ�Ϊv���ɶ��ܶ������ã�F����mg��R= ![]()
���v=3 ![]()
����v0= ![]() ����A�����˶��뿪�糡��B��һ����ײǰ�ٶ�Ϊ3
����A�����˶��뿪�糡��B��һ����ײǰ�ٶ�Ϊ3 ![]()
��2���⣺��AB��ײ��A��B���ٶȷֱ�ΪvA��vB
B��պõ�����ߵ㣬���ʱvB=0
��B���ɶ��ܶ������é�mg2R=0�� ![]()
A��B��ײ�������غ㣬��mv=mvA+mvB
�������vA= ![]() ��vB=2
��vB=2 ![]()
A�� B��ײ��������ʧ�Ļ�е�ܡ�E= ![]()
��á�E=2mgR
����v0= ![]() ��A��B��һ����ײ��B��պ��ܵ�����ߵ㣬��AB��ײ��������ʧ��е��Ϊ2mgR
��A��B��һ����ײ��B��պ��ܵ�����ߵ㣬��AB��ײ��������ʧ��е��Ϊ2mgR
��3���⣺��A���ٶ�Ϊv1ʱ�������糡���ٶȴ�СΪvB=2 ![]() ��B��Խ����ߵ��A�������A�ٴ���ײ��A�����ٽ���糡���ɶ��ܶ����ã�
��B��Խ����ߵ��A�������A�ٴ���ײ��A�����ٽ���糡���ɶ��ܶ����ã�
FR��fR= ![]()
���v1= ![]()
������ ![]() ��A���Ҳ��뿪�糡���ڵ糡�е�·��ΪR
��A���Ҳ��뿪�糡���ڵ糡�е�·��ΪR
��A���ٶ�С��v1��AB����B�����˶�����ߵ㣬������A�ٴ���ײ��A���ٴν���糡����A�ٶ�Ϊv2ʱ�պÿ��Դ�����뿪�糡���ɶ��ܶ����ã���f2R=0�� ![]() �����v2=
�����v2= ![]()
������ ![]() ʱ��A�ڵ糡�е�·��Ϊ2R
ʱ��A�ڵ糡�е�·��Ϊ2R
������A���ٶ�0��v0�� ![]() ʱ��A���ս�ͣ�ڵ糡�Ҳ�߽磬�ɶ��ܶ����ã�FR��fS
ʱ��A���ս�ͣ�ڵ糡�Ҳ�߽磬�ɶ��ܶ����ã�FR��fS ![]() =0��
=0�� ![]()
��� s=2R+ ![]()
�𣺽�B�ɵ���С��A��Bÿ����ײ�������ٶȣ���0��v0�� ![]() ��A�ڵ糡��ͨ������·����v0�Ĺ�ϵΪ�ټ�
��A�ڵ糡��ͨ������·����v0�Ĺ�ϵΪ�ټ� ![]() ��A���Ҳ��뿪�糡���ڵ糡�е�·��ΪR���ڼ�
��A���Ҳ��뿪�糡���ڵ糡�е�·��ΪR���ڼ� ![]() ʱ��A�ڵ糡�е�·��Ϊ2R�۵�A����0��v0��
ʱ��A�ڵ糡�е�·��Ϊ2R�۵�A����0��v0�� ![]() ʱ��s=2R+
ʱ��s=2R+ ![]()
����������1���ɶ��ܶ�����������ٶȣ���2���պõ�����ߵ㣬�ٶ�Ϊ�㣬�ɶ��ܶ���������������������ٶȣ����������غ㼴���ж���ʧ��е�ܣ���3�������ٶȲ�ͬʱ���������A�ڵ糡��ͨ������·����v0�Ĺ�ϵ��
�����㾫�������ն��ܶ������ۺ�Ӧ�úʹ����������������ڵ糡�е��˶��ǽ����ĸ�������Ҫ֪��Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ��������:��Һ�Ρ��͵Ρ�������С��ȣ�����˵������ȷ�İ�ʾ���⣬һ�㶼���ܺ������������ڴ�����������ǿ�糡�����ܵ糡�����������Ǻ�������˿��������ַ�������:�������ֽⷨ;�ڵ�Ч������������

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�