题目内容
如图所示,箱子a连同固定在箱子底部的竖直杆b的总质量M=10kg。箱子内部高度H=3.6m,杆长h=2.0m,杆的顶端为Q点。另有一内孔略大于直杆截面的铁环从箱子顶部P点以v0=4m/s的初速度落下,正好套在杆上沿杆运动,铁环第一次被箱子底部弹起后恰好能重新返回到P点,小铁环的质量为m=2kg。(不计铁环与箱底碰撞时的能量损失,g取10m/s2)

(1)求在沿杆运动的过程中,铁环受到的摩擦力f大小是多少?
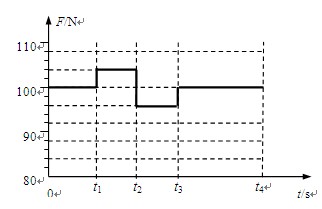
(2)设铁环在t0=0时刻释放,t1时刻第一次到达Q点,t2时刻第一次到达杆底部,t3时刻第二次到达Q点,t4时刻恰好回到P点。请在图(b)给定的坐标中,画出0~t4时间内箱子对地面压力的变化图像;
(3)求从开始下落到最终停止在箱底,铁环运动的总路程s是多少?
【答案】
在应用动能定理解题,并且还是多过程的运动,一定要注意各个过程中的始末状态
(1)f=4N(2)见解析(3)28.4m
【解析】
试题分析:(1)由-2fh = 0-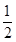 mv02
mv02
可求出f=4N(4分)
(2)(见右图)(4分)
(3)铁环第三次到达Q点时(向下 运动)的动能为Ek1=mg(H-h)=32J>2 fh
铁环第四次到达Q点时(向上运动)的动能为:
Ek2= Ek1-2 fh=16J,
设小环在空中再次上升的距离为h’,
-mgh’=0 -Ek2,可解得h’=0.8m(2分)
铁环第四次到达Q点时(向下运动)的动能为:Ek3= Ek2=16J ≤2 fh
之后铁环将始终沿直杆运动直至停止,设之后铁环沿直杆运动的距离为x
mgh-fx = 0-Ek3,可解出x=14m(2分)
(或者计算在杆上运动的总路程,结果为22m,也可得2分)
s=3H+h+2 h’+ x=28.4m(2分)
考点:考查了动能定理的应用
点评:
|
|
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图1示,箱子A连同固定在箱子底部的竖直杆的总质量为M=10kg.箱子内部高度H=3.75m,杆长h=2.5m,另有一质量为m=2kg的小铁环B套在杆上,从杆的底部以v0=10m/s的初速度开始向上运动,铁环B刚好能到达箱顶,不计空气阻力,g取10m/s2.求:
如图1示,箱子A连同固定在箱子底部的竖直杆的总质量为M=10kg.箱子内部高度H=3.75m,杆长h=2.5m,另有一质量为m=2kg的小铁环B套在杆上,从杆的底部以v0=10m/s的初速度开始向上运动,铁环B刚好能到达箱顶,不计空气阻力,g取10m/s2.求: 如图所示,箱子a连同固定在箱子底部的竖直杆b的总质量M=10kg.箱子内部高度H=3.6m,杆长h=2.0m,杆的顶端为Q点.另有一内孔略大于直杆截面的铁环从箱子顶部P点以v0=4m/s的初速度落下,正好套在杆上沿杆运动,铁环第一次被箱子底部弹起后恰好能重新返回到P点,小铁环的质量为m=2kg.(不计铁环与箱底碰撞时的能量损失,g取10m/s2)
如图所示,箱子a连同固定在箱子底部的竖直杆b的总质量M=10kg.箱子内部高度H=3.6m,杆长h=2.0m,杆的顶端为Q点.另有一内孔略大于直杆截面的铁环从箱子顶部P点以v0=4m/s的初速度落下,正好套在杆上沿杆运动,铁环第一次被箱子底部弹起后恰好能重新返回到P点,小铁环的质量为m=2kg.(不计铁环与箱底碰撞时的能量损失,g取10m/s2)

