题目内容
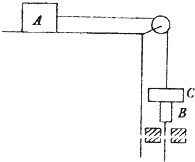如图所示，一条轻质细绳一端与A物体相连，另一端穿过C物体上的小孔后与B物体相连．它们的质量分别为mA=0.8kg．mB=mC=0.1kg，当B与C从静止开始下降h1=0.5m后，C被搁在平台上，B继续下降h2=0.3m后停止，求A与桌面之间的动摩因数多大？（不计滑轮及C小孔的摩擦）分析：先以A、B、C三个物体组成的系统为研究对象，对于B与C从静止开始下降h1=0.5m的过程中，运用能量守恒定律列式，可得到C物体刚被搁住时A、C的速度大小表达式；再对B继续下降h2=0.3m的过程，对于A、B组成的系统运用能量守恒列式，联立可求得A与桌面之间的动摩因数．
解答：解：设C物体刚被搁住时，A物体的速度为v，由能量守恒定律得
(mB+mC)gh1=
(mA+mB+mC)v2+Q1
其中Q1=μmAgh1．
对从C物体被搁住A物体在水平桌面上停止滑动，由能量守恒定律得
mBgh2+
(mA+mB)v2=Q2
其中Q2=μmAgh2．
联立以上四式，解得μ=0.2
答：A与桌面之间的动摩因数为0.2．
(mB+mC)gh1=
| 1 |
| 2 |
其中Q1=μmAgh1．
对从C物体被搁住A物体在水平桌面上停止滑动，由能量守恒定律得
mBgh2+
| 1 |
| 2 |
其中Q2=μmAgh2．
联立以上四式，解得μ=0.2
答：A与桌面之间的动摩因数为0.2．
点评：本题是连接体问题，运用能量守恒定律求解比较简便．由于A与B加速度大小相等，方向不同，也可采用隔离法研究加速度，由牛顿第二定律和运动学公式结合同样能解．
练习册系列答案
相关题目
（1）一个实验小组在“探究弹力和弹簧伸长的关系”的实验中，使用两条不同的轻质弹簧a和b，得到弹力与弹簧长度的图象如图所示．则：
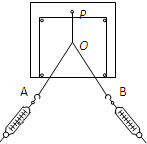
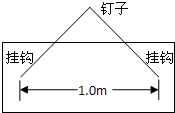如图所示，小洁要在客厅里挂上一幅质量为1.0kg的画（含画框），画框背面有两个相距1.0m、位置固定挂钩，她将轻质细绳两端分别固定在两个挂钩上，把画对称地挂在竖直墙壁的钉子上，挂好后整条细绳呈绷紧状态．设细绳能够承受最大拉力为10N，g取10m/s2，则细绳至少需要多长才不至于断掉？（ ）
如图所示，在质量为m=1kg的重物上系着一条长30cm的细绳，细绳的另一端连着一个轻质圆环，圆环套在水平的棒上可以滑动，环与棒间的动摩擦因数μ为0.75，另有一条细绳，在其一端跨过定滑轮，定滑轮固定在距离圆环50cm的地方，当细绳的端点挂上重物G，而圆环将要开始滑动时，（g取10/ms2）试问：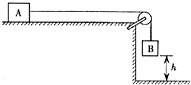
如图所示，在水平桌面的边角处有一轻质光滑的定滑轮，一条不可伸长的轻绳绕过定滑轮分别与物块A、B相连，细绳处于伸直状态，物块A和B的质量分别为mA=8kg和mB=2kg，物块A与水平桌面间的动摩擦因数μ=0.1，物块B距地面的高度h=0.15m．桌面上部分的绳子足够长．现将物块B从h高处由静止释放，直到A停止运动．（g取10m/s2）求：