题目内容
如图所示是建筑工地常用的一种“深穴打夯机”。工作时,电动机带动两个紧压夯杆的滚轮匀速转动将夯杆从深为h的坑中提上来,当两个滚轮彼此分开时,夯杆被释放,最后夯在自身重力作用下,落回深坑,夯实坑底。然后两个滚轮再次压紧,夯杆再次被提上来,如此周而复始工作。已知两个滚轮边缘线速度v恒为4 m/s,每个滚轮对夯杆的正压力Fn=2×104,滚轮与夯杆间的动摩擦因数μ=0.3,夯杆质量m=1×103 kg,坑深h=6.4 m。假定在打夯的过程中坑的深度变化及夯与坑底的作用时间均忽略不计,且夯杆底端升到坑口时,速度恰好为零。取g=10 m/s2,求:
(1)夯杆上升过程中被滚轮释放时的速度为多大?此时夯杆底端离坑底多高?
(2)每个打夯周期中,电动机对夯杆所做的功?
(3)打夯周期是多少?
解:(1)f1=2μFN=1.2×104 N;
a1=![]() =2 m/s2
=2 m/s2
当夯杆与滚轮相对静止时:v=a1t1=4 m/s,t1=2 s,
h1=![]() a1t21=4 m
a1t21=4 m
当夯杆以v=4 m/s的初速度竖直上抛,上升高度为:
h2=![]() =0.8 m
=0.8 m
则当夯杆加速向上运动速度到达v=4 m/s后,夯杆匀速上升,匀速上升高度为:
h3=h-h1-h2=1.6 m
因此,夯杆先匀加速上升,后匀速上升,再竖直上抛。
故夯杆上升过程中被滚轮释放时的速度为4 m/s;
此时夯杆底端离坑底高度Δh=h-h2=5.6 m。
(2)W=mgh=6.4×104 J。
(3)夯杆竖直上抛运动的时间为:t2=![]() =0.4 s
=0.4 s
夯杆匀速上升的时间为:t3=![]() =0.4 s
=0.4 s
夯杆自由落体的时间为:h=![]() gt42,t4=
gt42,t4=![]() =1.13 s
=1.13 s
故打夯周期为:T=t1+t2+t3+t4=3.93 s。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
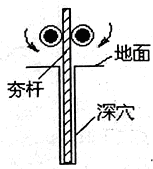 如图所示是建筑工地常用的一种“深穴打夯机”,电动机带动两个滚轮匀速转动将静止的夯杆从深坑提上来,当夯杆底端刚到达坑口时,两个滚轮彼此分开,将夯杆释放,夯杆在重力作用下落回深坑,夯实坑底.如此循环往复.已知两个滚轮边缘的线速度恒为v=4m/s,每个滚轮对夯杆的压力FN=2×104N,滚轮与夯杆间的动摩擦因数μ=0.3,夯杆质量m=1×103kg,坑深h=6.4m,取g=10m/s2.求:
如图所示是建筑工地常用的一种“深穴打夯机”,电动机带动两个滚轮匀速转动将静止的夯杆从深坑提上来,当夯杆底端刚到达坑口时,两个滚轮彼此分开,将夯杆释放,夯杆在重力作用下落回深坑,夯实坑底.如此循环往复.已知两个滚轮边缘的线速度恒为v=4m/s,每个滚轮对夯杆的压力FN=2×104N,滚轮与夯杆间的动摩擦因数μ=0.3,夯杆质量m=1×103kg,坑深h=6.4m,取g=10m/s2.求: 如图所示是建筑工地常用的一种“深穴打夯机”.工作时,电动机带动两个紧压夯杆的滚轮匀速运转将夯杆从深为h的坑中提上来,当两个滚轮彼此分开时,夯杆被释放,最后夯杆在自身的重力作用下,落回深坑夯实坑底.然后,两个滚轮再次压紧夯杆,夯杆再次被提上来,如此周而复始工作.已知两个滚轮的半径为R=40cm,角速度ω=10rad/s,每个滚轮对夯杆的正压力FN=2×104 N,滚轮与夯杆的动摩擦因数?=0.3,夯杆质量m=1×103 kg,坑深h=6.4m.假定在打夯的过程中坑的深度不变,且夯杆底端刚到坑口时,速度恰好为零.取g=10m/s2,
如图所示是建筑工地常用的一种“深穴打夯机”.工作时,电动机带动两个紧压夯杆的滚轮匀速运转将夯杆从深为h的坑中提上来,当两个滚轮彼此分开时,夯杆被释放,最后夯杆在自身的重力作用下,落回深坑夯实坑底.然后,两个滚轮再次压紧夯杆,夯杆再次被提上来,如此周而复始工作.已知两个滚轮的半径为R=40cm,角速度ω=10rad/s,每个滚轮对夯杆的正压力FN=2×104 N,滚轮与夯杆的动摩擦因数?=0.3,夯杆质量m=1×103 kg,坑深h=6.4m.假定在打夯的过程中坑的深度不变,且夯杆底端刚到坑口时,速度恰好为零.取g=10m/s2,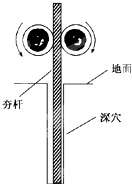 如图所示是建筑工地常用的一种“深穴打夯机”.工作时,电动机带动两个紧压夯杆的滚轮匀速转动将夯杆从深为h的坑中提上来,当两个滚轮彼此分开时,夯杆被释放,最后夯在自身重力作用下,落回深坑,夯实坑底.然后两个滚轮再次压紧,夯杆再次被提上来,如此周而复始工作.已知两个滚轮边缘线速度v恒为4m/s,每个滚轮对夯杆的正压力FN=2×104N,滚轮与夯杆间的动摩擦因数μ=0.3,夯杆质量m=1×103kg,坑深h=6.4m.假定在打夯的过程中坑的深度变化及夯与坑底的作用时间均忽略不计,且夯杆底端升到坑口时,速度恰好为零.取g=10m/s2,求:
如图所示是建筑工地常用的一种“深穴打夯机”.工作时,电动机带动两个紧压夯杆的滚轮匀速转动将夯杆从深为h的坑中提上来,当两个滚轮彼此分开时,夯杆被释放,最后夯在自身重力作用下,落回深坑,夯实坑底.然后两个滚轮再次压紧,夯杆再次被提上来,如此周而复始工作.已知两个滚轮边缘线速度v恒为4m/s,每个滚轮对夯杆的正压力FN=2×104N,滚轮与夯杆间的动摩擦因数μ=0.3,夯杆质量m=1×103kg,坑深h=6.4m.假定在打夯的过程中坑的深度变化及夯与坑底的作用时间均忽略不计,且夯杆底端升到坑口时,速度恰好为零.取g=10m/s2,求: