��Ŀ����
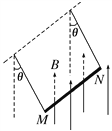
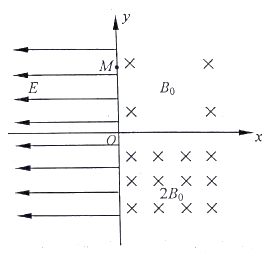
����Ŀ����ͼ��ʾ����y��������һƽ��x�᷽�����ǿ�糡���糡ǿ��![]() ����y���Ҳ���ڴ�ֱֽ���������ǿ �ų�����һ�����ڴų��ĴŸ�Ӧǿ�ȴ�С
����y���Ҳ���ڴ�ֱֽ���������ǿ �ų�����һ�����ڴų��ĴŸ�Ӧǿ�ȴ�С![]() �����������ڴų��ĴŸ�Ӧǿ�ȴ�СΪ
�����������ڴų��ĴŸ�Ӧǿ�ȴ�СΪ![]() ������һ�Ⱥ�
������һ�Ⱥ�![]() �������У��ӵ糡����y�����10cm��P�㣨ͼ��δ������ɾ�ֹ�ͷţ������˶�һ��ʱ����M�����ų�����һֱ�ڴų����˶��Ҷ�δ�ֱͨ��x�ᣬ������������������
�������У��ӵ糡����y�����10cm��P�㣨ͼ��δ������ɾ�ֹ�ͷţ������˶�һ��ʱ����M�����ų�����һֱ�ڴų����˶��Ҷ�δ�ֱͨ��x�ᣬ������������������
��1�����ӽ���ų�ʱ���ٶȴ�С��
��2�������ӽ���ų���ʼ��ʱ�����ӵ����ε���x����������ʱ�䣻
��3�����ӹ켣��һ�γ����ཻʱ����Ӧ�Ľ������ꡣ
���𰸡���1��2��104m/s��2��![]() �С�10-4s ��3��P��
��10-4s ��3��P��![]() m��
m�� ![]() m��
m��
�������������������1�������ڵ糡�м��ٺ����ų������ڵ糡���ɶ��ܶ�����������ӽ���ų�ʱ���ٶȴ�С����2�����ӽ���ų�������Բ���˶����������˶��켣ͼ�����������ڴų���ƫת�Ĺ��ɼ����������ӽ���ų���ʼ��ʱ�����ӵ����ε���x����������ʱ������3���������ӵ��˶��켣ͼ�ͼ��ι�ϵ����������ӹ켣��һ�γ����ཻʱ����Ӧ�Ľ�������.
��1���������ڵ糡�У��ɶ��ܶ���![]()
�� ![]()
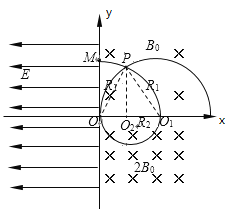
��2�����ӽ���ų�������Բ���˶����켣��ͼ��ʾ
������������ʽ�� ![]()
��![]()
�ã� ![]()
![]()
�������Ӵӽ���ų����������˶���x�����õ�ʱ��Ϊ![]()
������ֵ�ɵ�![]()
��3�������ӵ�һ�γ����ཻʱ�Ĺ켣����ΪP����ͼ��ʾ

��ͼ��֪��������![]() Ϊ�ȱ������Σ����У�
Ϊ�ȱ������Σ����У� ![]()
������������ʽ�У� ![]() �������
������� ![]()
���ݼ��ι�ϵ�ɵã�P������![]() ��
�� ![]()
����P������ΪP��![]() ��
��