题目内容
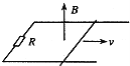
【题目】某校兴趣小组制作了一个游戏装置,其简化模型如图所示,在A点用一弹射装置可将静止的小滑块以v0水平速度弹射出去,沿水平直线轨道运动到B点后,进入半径R=0.1m的光滑竖直圆形轨道,运行一周后自B点向C点运动,C点右侧有一陷阱,C、D两点的竖直高度差h=0.2m,水平距离s=0.6m,水平轨道AB长为L1=0.5m,BC长为L2=1.5m,小滑块与水平地面间的动摩擦因数μ=0.4,重力加速度g=10m/s2.
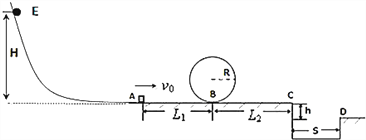
(1)若小滑块恰能通过圆形轨道的最高点,求小滑块在A点弹射出的速度大小;
(2)若游戏规则为小滑块沿着圆形轨道运行一周离开圆形轨道后只要不掉进陷阱即为胜出.求小滑块在A点弹射出的速度大小范围;
(3)若小滑块是与从光滑斜轨道E点静止释放的小球发生完全非弹性碰撞后,离开A点的(小球质量与小滑块的质量相等,且均可视为质点,斜轨道与水平地面平滑连接),求当满足(2)中游戏规则时,释放点E与过A水平面的竖直高度H的大小范围.
【答案】(1)v1=3m/s (2) 3m/s≤vA≤4m/s和vA≥5m/s (3) 1.8m≤H≤3.2m和H≥5m
【解析】试题分析:小球恰能通过圆形轨道的最高点,由重力提供向心力,由牛顿第二定律可求出小球经圆形轨道的最高点时的速度,根据动能定理求解小球在A点的初速度;若小球既能通过圆形轨道的最高点,又不能掉进壕沟,有两种情况:第一种情况:小球停在BC间;第二种情况:小球越过壕沟.若小球恰好停在C点,由动能定理求出小球的初速度.得出第一种情况下小球初速度范围.若小球恰好越过壕沟,由平抛运动知识求出小球经过C点的速度,再由动能定理求出初速度,得到初速度范围。
(1)小滑块恰能通过圆轨道最高点的速度为v,
由牛顿第二定律:![]()
由B到最高点小滑块机械能,由动能定理得: ![]()
由A到B根据动能定理得: ![]()
联立以上解得A点的速度为:v1=3m/s
(2) 若小滑块能通过C点并恰好越过壕沟,滑块离开C点后做平抛运动,
竖直方向: ![]()
水平方向:s=vct
从A到C过程,由动能定理得: ![]()
解得:v3=5m/s,
所以初速度的范围为:vA≥5m/s