Question

．如图所示，V形细杆AOB能绕其对称轴OO’转动，OO’沿竖直方向，V形杆的两臂与转轴间的夹角均为=45°。两质量均为m=0.1kg的小环，分别套在V形杆的两臂上，并用长为l=1.2m、能承受最大拉力F_max=4.5N的轻质细线连结，环与臂间的最大静摩擦力等于两者间弹力的0.2倍。当杆以角速度ω转动时，细线始终处于水平状态，取g=10m/s²。

（1）求杆转动角速度ω的最小值；

（2）将杆的角速度从（1）问中求得的最小值开始缓慢增大，直到细线断裂，写出此过程中细线拉力随角速度变化的函数关系式。

Answer 1

（1）3.33rad/s

（2）

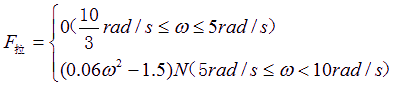
解析:

（1）∵角速度最小时，f_max沿杆向上，则

且，

∴ω₁=10/3≈3.33rad/s      6分

（2）当f_max沿杆向下时，有

∴ω₂=5rad/s

当细线拉力刚达到最大时，有

∴ω₃=10rad/s

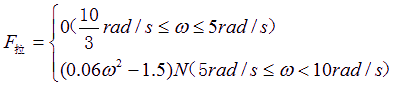∴（8分）