题目内容
14.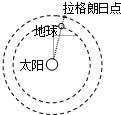 2011年8月,“嫦娥二号”成功进入环绕“日地拉格朗日点”的轨道,我国成为世界上第三个造访该点的国家.如图所示,该拉格朗日点位于太阳和地球连线的延长线上,一飞行器处于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动,若地球公转的周期为T,公转轨道半径为R,地球与飞行器间的距离为r,求:
2011年8月,“嫦娥二号”成功进入环绕“日地拉格朗日点”的轨道,我国成为世界上第三个造访该点的国家.如图所示,该拉格朗日点位于太阳和地球连线的延长线上,一飞行器处于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动,若地球公转的周期为T,公转轨道半径为R,地球与飞行器间的距离为r,求:(1)此飞行器在该拉格朗日点的运行速度;
(2)在地球和太阳所在的直线上还有这样的点(飞行器处于该点,集合不消耗燃料的情况下与地球同步绕太阳做圆周运动)吗?写出你的分析过程.
分析 飞行器与地球同步绕太阳运动,角速度相等,飞行器靠太阳和地球引力的合力提供向心力.
根据圆周运动求解此飞行器在该拉格朗日点的运行速度.
解答 解:(1)飞行器与地球同步绕太阳运动,角速度相等,周期相等,
地球公转的周期为T,公转轨道半径为R,地球与飞行器间的距离为r,
所以此飞行器在该拉格朗日点的运行速度v=$\frac{2π(R+r)}{T}$
(2)飞行器的向心力由太阳和地球引力的合力提供,$\frac{GMm}{{r}^{2}}$+$\frac{GM′m}{{(R+r)}^{2}}$=mrω2,
飞行器与地球同步绕太阳运动,角速度相等,为一定值,
所以除去图中的“日地拉格朗日点”外,则在“日-地”连线上具有上述功能的点的个数为0,
答:(1)此飞行器在该拉格朗日点的运行速度是$\frac{2π(R+r)}{T}$
(2)在地球和太阳所在的直线上没有这样的点.
点评 本题考查万有引力的应用,题目较为新颖,在解题时要注意分析向心力的来源及题目中隐含的条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4. 如图所示,两根平行放置、长度很长的直导线A和B,放置在与导线所在平面垂直的匀强磁场中,A导线通有电流I、B导线通有电流2I,且电流方向相反,研究两导线中正相对的长度均为L的两小段导线a、b.导线a受到磁场力大小为F1,导线b受到的磁场力大小为F2,则A通电导线的电流在b导线处产生的磁感应强度大小为( )
如图所示,两根平行放置、长度很长的直导线A和B,放置在与导线所在平面垂直的匀强磁场中,A导线通有电流I、B导线通有电流2I,且电流方向相反,研究两导线中正相对的长度均为L的两小段导线a、b.导线a受到磁场力大小为F1,导线b受到的磁场力大小为F2,则A通电导线的电流在b导线处产生的磁感应强度大小为( )
 如图所示,两根平行放置、长度很长的直导线A和B,放置在与导线所在平面垂直的匀强磁场中,A导线通有电流I、B导线通有电流2I,且电流方向相反,研究两导线中正相对的长度均为L的两小段导线a、b.导线a受到磁场力大小为F1,导线b受到的磁场力大小为F2,则A通电导线的电流在b导线处产生的磁感应强度大小为( )
如图所示,两根平行放置、长度很长的直导线A和B,放置在与导线所在平面垂直的匀强磁场中,A导线通有电流I、B导线通有电流2I,且电流方向相反,研究两导线中正相对的长度均为L的两小段导线a、b.导线a受到磁场力大小为F1,导线b受到的磁场力大小为F2,则A通电导线的电流在b导线处产生的磁感应强度大小为( )| A. | $\frac{{F}_{2}}{2IL}$ | B. | $\frac{{F}_{1}}{IL}$ | C. | $\frac{2{F}_{1}-{F}_{2}}{2IL}$ | D. | $\frac{2{F}_{1}-{F}_{2}}{IL}$ |
5.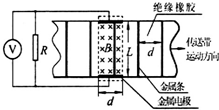 某校科技小组的同学设计了一个传送带测速仪,测速原理如图所示.在传送带(绝缘橡胶)一端的下方固定有间距为L、长度为d的平行金属电极.电极间充满磁感应强度为B、方向垂直传送带平面(纸面)向里、有理想边界的匀强磁场,且电极之间接有理想电压表和电阻R.传送带背面固定有若干根间距为d的平行细金属条,其电阻均为r.传送带运行过程中始终仅有一根金属条处于磁场中且与电极良好接触.当传送带以一定的速度匀速运动时,电压表的示数为U.则下列说法中正确的是( )
某校科技小组的同学设计了一个传送带测速仪,测速原理如图所示.在传送带(绝缘橡胶)一端的下方固定有间距为L、长度为d的平行金属电极.电极间充满磁感应强度为B、方向垂直传送带平面(纸面)向里、有理想边界的匀强磁场,且电极之间接有理想电压表和电阻R.传送带背面固定有若干根间距为d的平行细金属条,其电阻均为r.传送带运行过程中始终仅有一根金属条处于磁场中且与电极良好接触.当传送带以一定的速度匀速运动时,电压表的示数为U.则下列说法中正确的是( )
 某校科技小组的同学设计了一个传送带测速仪,测速原理如图所示.在传送带(绝缘橡胶)一端的下方固定有间距为L、长度为d的平行金属电极.电极间充满磁感应强度为B、方向垂直传送带平面(纸面)向里、有理想边界的匀强磁场,且电极之间接有理想电压表和电阻R.传送带背面固定有若干根间距为d的平行细金属条,其电阻均为r.传送带运行过程中始终仅有一根金属条处于磁场中且与电极良好接触.当传送带以一定的速度匀速运动时,电压表的示数为U.则下列说法中正确的是( )
某校科技小组的同学设计了一个传送带测速仪,测速原理如图所示.在传送带(绝缘橡胶)一端的下方固定有间距为L、长度为d的平行金属电极.电极间充满磁感应强度为B、方向垂直传送带平面(纸面)向里、有理想边界的匀强磁场,且电极之间接有理想电压表和电阻R.传送带背面固定有若干根间距为d的平行细金属条,其电阻均为r.传送带运行过程中始终仅有一根金属条处于磁场中且与电极良好接触.当传送带以一定的速度匀速运动时,电压表的示数为U.则下列说法中正确的是( )| A. | 传送带匀速运动的速率为$\frac{U}{BL}$ | |
| B. | 电阻R产生焦耳热的功率为$\frac{U^2}{R+r}$ | |
| C. | 金属条经过磁场区域受到的安培力大小为$\frac{BUd}{R+r}$ | |
| D. | 每根金属条经过磁场区域的全过程中克服安培力做功为$\frac{BLUd}{R}$ |
2.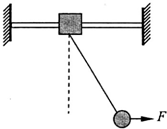 如图所示,滑块穿在水平横杆上并可沿杆左右滑动,它的下端通过一根细线与小球相连,小球受到水平向右的拉力F的作用,此时滑块与小球处于静止状态.保持拉力F始终沿水平方向,将其大小缓慢增大,细线偏离竖直方向的角度将增大,这一过程中滑块始终保持静止,则( )
如图所示,滑块穿在水平横杆上并可沿杆左右滑动,它的下端通过一根细线与小球相连,小球受到水平向右的拉力F的作用,此时滑块与小球处于静止状态.保持拉力F始终沿水平方向,将其大小缓慢增大,细线偏离竖直方向的角度将增大,这一过程中滑块始终保持静止,则( )
 如图所示,滑块穿在水平横杆上并可沿杆左右滑动,它的下端通过一根细线与小球相连,小球受到水平向右的拉力F的作用,此时滑块与小球处于静止状态.保持拉力F始终沿水平方向,将其大小缓慢增大,细线偏离竖直方向的角度将增大,这一过程中滑块始终保持静止,则( )
如图所示,滑块穿在水平横杆上并可沿杆左右滑动,它的下端通过一根细线与小球相连,小球受到水平向右的拉力F的作用,此时滑块与小球处于静止状态.保持拉力F始终沿水平方向,将其大小缓慢增大,细线偏离竖直方向的角度将增大,这一过程中滑块始终保持静止,则( )| A. | 滑块对杆的压力增大 | B. | 滑块受到杆的摩擦力增大 | ||
| C. | 小球受到细线的拉力大小不变 | D. | 小球所受各力的合力增大 |
9.下列说法正确的是( )
| A. | 温度升高,物体分子热运动的平均动能一定增大 | |
| B. | 当分子力表现为斥力时,分子势能随分子间距离的减小而减小 | |
| C. | 外界对物体做功,物体内能一定增加 | |
| D. | 对于一定质量的理想气体,如果压强不变,体积增大,那么它一定从外界吸热 |
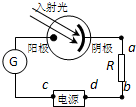
19.如图为光电管工作原理示意图,入射光的光子能量为hν,阴极材料的逸出功为W,当G表偏转时,则( )

| A. | hν<W | |
| B. | 流过电阻R的电流方向是b流向a | |
| C. | 增大入射光的频率,光电子逸出的初动能增大 | |
| D. | 减弱入射光强度,ab两端的电压减小 |
3.某同学家一台新电冰箱能显示冷藏室内的温度,存放食物之前该同学进行试通电,该同学将打开的冰箱密封门关闭并给冰箱通电.若大气压为1.0×105Pa,刚通电时显示温度为27℃,通电一段时间后显示温度为7℃,则此时密封的冷藏室中气体的压强是( )
| A. | 0.26×105Pa | B. | 0.93×105Pa | C. | 1.07×105Pa | D. | 3.86×105Pa |
15.如图甲所示,O为振源,OP=s,t=0时刻O点由平衡位置开始振动,产生向右沿直线传播的简谐横波.图乙为从t=0时刻开始描绘的P点的振动图象.下列判断中正确的是( )


| A. | 该波的传播速度v=$\frac{s}{{t}_{2}-{t}_{1}}$ | |
| B. | 这列波的波长λ=$\frac{s({t}_{2}-{t}_{1})}{{t}_{1}}$ | |
| C. | t=0时刻,振源O振动的方向沿y轴正方向 | |
| D. | P点在$\frac{{t}_{2}+3{t}_{1}}{4}$时刻处于波峰位置 | |
| E. | t1时刻,P点的振动方向沿y轴负方向 |
 如图所示,质量m=10kg的木箱静止在水平地面上,现用F=100N的水平拉力拉木箱,当木箱移动10m的撤去拉力.已知木箱与地面间的动摩擦因数μ=0.4,重力加速度g取10m/s2,试求:
如图所示,质量m=10kg的木箱静止在水平地面上,现用F=100N的水平拉力拉木箱,当木箱移动10m的撤去拉力.已知木箱与地面间的动摩擦因数μ=0.4,重力加速度g取10m/s2,试求: