题目内容
 如图所示,虚线MN为电场、磁场的分界线,匀强电场E=103V/m,方向竖直向上,电场线与边界线MN成45°角,匀强磁场垂直纸面向里,磁感应强度B=1T,在电场中有一点A,A点到边界线MN的垂直距离AO=10cm,将比荷为
如图所示,虚线MN为电场、磁场的分界线,匀强电场E=103V/m,方向竖直向上,电场线与边界线MN成45°角,匀强磁场垂直纸面向里,磁感应强度B=1T,在电场中有一点A,A点到边界线MN的垂直距离AO=10cm,将比荷为| 2 |
(1)粒子第一次进入磁场时的速度大小;
(2)粒子从释放到下一次进入到电场区域所需要的时间;
(3)粒子第二次进、出磁场处两点间的距离.
分析:(1)根据动能定理求解粒子第一次进入磁场时的速度大小;
(2)先求出粒子在电场中匀加速直线运动的时间,由牛顿第二定律和速度公式结合求解;粒子在磁场中转过
周,运动时间为
T,求得周期T,即求出在磁场中运动时间,从而得到总时间;
(3)画出轨迹,根据几何知识求解粒子第二次进、出磁场处两点间的距离.
(2)先求出粒子在电场中匀加速直线运动的时间,由牛顿第二定律和速度公式结合求解;粒子在磁场中转过
| 3 |
| 4 |
| 3 |
| 4 |
(3)画出轨迹,根据几何知识求解粒子第二次进、出磁场处两点间的距离.
解答: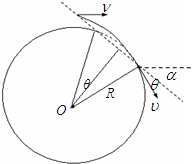 解:(1)粒子在电场中做初速度为0的匀加速直线运动,设粒子的质量为m,带电量为q,进入磁场时的速度为v,
解:(1)粒子在电场中做初速度为0的匀加速直线运动,设粒子的质量为m,带电量为q,进入磁场时的速度为v,
则:
qElAO=
mv2
代入数据解得:v=2×103m/s
(2)设粒子在进入磁场前匀加速运动的时间为t1,在磁场中做匀速圆周运动的时间为t2,
则 t1=
,a=
得 t1=
=
×10-4s
周期T=
,则t2=
T=
×10-4s
所以总时间为 t总=t1+t2=
(1+
)×10-4s
(3)如图所示,粒子在电场中做类平抛运动,设粒子第二次进入磁场时的速度为V,速度方向与水平方向间的夹角为α,与分界线间的夹角为θ,则有:
tanα=2
θ=α-45°
V=
=
v
半径R=
=
m
粒子第二次进、出磁场处两点间的距离
l=2Rsinθ=2Rsin(α-45°)
解得,l=0.2m
答:
(1)粒子第一次进入磁场时的速度大小是2×103m/s;
(2)粒子从释放到下一次进入到电场区域所需要的时间是
(1+
)×10-4s;
(3)粒子第二次进、出磁场处两点间的距离是0.2m.
 解:(1)粒子在电场中做初速度为0的匀加速直线运动,设粒子的质量为m,带电量为q,进入磁场时的速度为v,
解:(1)粒子在电场中做初速度为0的匀加速直线运动,设粒子的质量为m,带电量为q,进入磁场时的速度为v,则:
| 2 |
| 1 |
| 2 |
代入数据解得:v=2×103m/s
(2)设粒子在进入磁场前匀加速运动的时间为t1,在磁场中做匀速圆周运动的时间为t2,
则 t1=
| v |
| a |
| Eq |
| m |
得 t1=
| mv |
| qB |
| ||
| 4 |
周期T=
| 2πm |
| qB |
| 3 |
| 4 |
3
| ||
| 4 |
所以总时间为 t总=t1+t2=
| 2 |
| 3π |
| 4 |
(3)如图所示,粒子在电场中做类平抛运动,设粒子第二次进入磁场时的速度为V,速度方向与水平方向间的夹角为α,与分界线间的夹角为θ,则有:
tanα=2
θ=α-45°
V=
| v |
| cosα |
| 5 |
半径R=
| mV |
| qB |
| ||
| 10 |
粒子第二次进、出磁场处两点间的距离
l=2Rsinθ=2Rsin(α-45°)
解得,l=0.2m
答:
(1)粒子第一次进入磁场时的速度大小是2×103m/s;
(2)粒子从释放到下一次进入到电场区域所需要的时间是
| 2 |
| 3π |
| 4 |
(3)粒子第二次进、出磁场处两点间的距离是0.2m.
点评:本题的解题关键是画出磁场中的轨迹,根据几何知识求出距离与半径,确定轨迹的圆心角,计算时间与周期的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,虚线MN左侧的整个空间存在一方向竖直向下的匀强电场E1,虚线右侧的整个空间存在方向竖直向上的匀强电场E2和方向垂直纸面向内的匀强磁场B.一绝缘带电小球从距MN左侧的A点以一定的初速度向右运动,进入虚线右侧后在竖直面内做匀速圆周运动,向左穿过MN后恰好落回A点.已知A点到MN 的距离为L;小球的质量为m、带电量为q,小球的初速度为v0,小球与水平面的动摩擦因数μ=v02/4gL;E1=mg/2q.
如图所示,虚线MN左侧的整个空间存在一方向竖直向下的匀强电场E1,虚线右侧的整个空间存在方向竖直向上的匀强电场E2和方向垂直纸面向内的匀强磁场B.一绝缘带电小球从距MN左侧的A点以一定的初速度向右运动,进入虚线右侧后在竖直面内做匀速圆周运动,向左穿过MN后恰好落回A点.已知A点到MN 的距离为L;小球的质量为m、带电量为q,小球的初速度为v0,小球与水平面的动摩擦因数μ=v02/4gL;E1=mg/2q. 如图所示,虚线MN下方存在竖直向上的匀强电场,场强E=2×103V/m,电场区域上方有一竖直放置长为l=0.5m的轻质绝缘细杆,细杆的上下两端分别固定一个带电小球A、B,它们的质量均为m=0.01kg,A带正电,电量为q1=2.5×10-4C;B带负电,电荷量q2=5×10-5C,B到MN的距离h=0.05m.现将轻杆由静止释放(g取10m/s2),求:
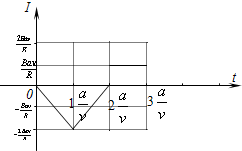
如图所示,虚线MN下方存在竖直向上的匀强电场,场强E=2×103V/m,电场区域上方有一竖直放置长为l=0.5m的轻质绝缘细杆,细杆的上下两端分别固定一个带电小球A、B,它们的质量均为m=0.01kg,A带正电,电量为q1=2.5×10-4C;B带负电,电荷量q2=5×10-5C,B到MN的距离h=0.05m.现将轻杆由静止释放(g取10m/s2),求: 如图所示,虚线MN为匀强磁场中的一条分界线,与虚线JK的夹角为45°,MN左边的磁场垂直纸面向外,MN右边的磁场垂直纸面向里,右边界为虚线LK,两边磁场的磁感应强度大小都为B.正方形线框PQRS边长为a,以速度v由左向右沿JK方向在磁场中做匀速直线运动.t=0时刻Q点刚好到达MN线上,规定线框中顺时针方向电流为正向电流,则线框中感应电流随时间变化的图象应为( )
如图所示,虚线MN为匀强磁场中的一条分界线,与虚线JK的夹角为45°,MN左边的磁场垂直纸面向外,MN右边的磁场垂直纸面向里,右边界为虚线LK,两边磁场的磁感应强度大小都为B.正方形线框PQRS边长为a,以速度v由左向右沿JK方向在磁场中做匀速直线运动.t=0时刻Q点刚好到达MN线上,规定线框中顺时针方向电流为正向电流,则线框中感应电流随时间变化的图象应为( )